Урок-экскурсия по картине Н.П. Богданова-Бельского "Устный счет". Устный счет картина
Богданов–Бельский. Устный счет в народной школе — что на самом деле изображено на картине: 101
Многие видели картину "Устный счет в народной школе". Конец 19 века, народная школа, доска, интеллигентный учитель, бедно одетые дети, 9–10 лет, с энтузиазмом пытаются решить в уме задачу написанную на доске. Первый решивший сообщает ответ учителю на ухо, шепотом, чтобы другие не потеряли интерес.
Теперь посмотрим на задачу: ( 10 в квадрате + 11 в квадрате + 12 в квадрате + 13 в квадрате + 14 в квадрате) / 365 =???
Черт! Черт! Черт! Наши дети в возрасте 9 лет не решат такую задачу, уж во всяком случае в уме! Почему чумазых и босоногих деревенских детей в деревянной школе из одной комнаты учили так хорошо, а наших детей учат так плохо?!
Не спешите возмущаться. Приглядитесь к картине. Вам не кажется, что учитель выглядит слишком интеллигентно, как–то по–профессорски, и одет с явной претензией? Почему в школьном классе такой высокий потолок и дорогущая печь с белыми кафельными изразцами? Неужели так выглядели деревенские школы и учителя в них?
Разумеется, выглядели они не так. Картина называется "Устный счет в народной школе С.А.Рачинского". Сергей Рачинский — профессор ботаники Московского университета, человек с определенными правительственными связями (например, приятель обер–прокурора Синода Победоносцева), помещик — в середине жизни бросил все дела, уехал в свое имение (Татево в Смоленской губернии) и завел там (разумеется, за свой счет) экспериментальную народную школу.
Школа была одноклассной, что отнюдь не значило, что в ней учат один год. В такой школе учили тогда 3–4 года (а в двухклассных школах — 4–5 лет, в трехклассных — 6 лет). Слово одноклассный означало то, что дети трех лет обучения составляют единый класс, и один учитель занимается с ними со всеми в пределах одного урока. Это было достаточно хитрое дело: пока дети одного года обучения делали какое–нибудь письменное упражнение, дети второго года отвечали у доски, дети третьего года читали учебник и т.п., и учитель попеременно уделял внимание каждой группе.
Педагогическая теория Рачинского была весьма оригинальной, и разные ее части как–то плохо сходились друг с другом. Во–первых, основой образования для народа Рачинский считал обучение церковно–славянскому языку и Закон Божий, причем не столько объяснительный, сколько состоящий в заучивании молитв. Рачинский твердо верил, что знающий наизусть определенное количество молитв ребенок непременно вырастет высоконравственным человеком, причем сами звуки церковно–славянского языка уже окажут улучшающее нравственность воздействие. Для практики в языке Рачинский рекомендовал детям наниматься читать Псалтирь над покойниками (sic!).
Во–вторых, Рачинский считал, что крестьянам полезно и нужно быстро считать в уме. Преподаванием математической теории Рачинский интересовался мало, а вот устный счет в своей школе он поставил очень хорошо. Ученики твердо и быстро отвечали, сколько сдачи с рубля надо дать тому, кто покупает 6 3/4 фунта моркови по 8 1/2 копейки за фунт. Возведение в квадрат, изображенное на картине, было самой сложной математической операцией, изучавшейся в его школе.
И наконец, Рачинский был сторонником очень практичного преподавания русского языка — от учеников не требовалось ни особенных навыков правописания, ни хорошего почерка, теоретической грамматике их вообще не учили. Главное было научиться бегло читать и писать, пусть корявым почерком и не слишком грамотно, но понятно, то, что может пригодиться крестьянину в быту: простые письма, прошения и пр. Еще в школе Рачинского преподавался кой–какой ручной труд, дети пели хором, и на этом всё образование и заканчивалось.
Рачинский был настоящим энтузиастом. Школа стала всей его жизнью. Дети у Рачинского жили в общежитии и были организованы в коммуну: они выполняли все работы по хозяйственному обслуживанию самих себя и школы. Рачинский, не имевший семьи, проводил с детьми всё время с раннего утра до позднего вечера, а так как он был очень добрый, благородный и искренне привязанный к детям человек, его влияние на учеников было огромным. Кстати, первому решившему задачу ребенку Рачинский выдавал пряник (в буквальном смысле слова, кнута же у него не было).
Сами школьные занятия занимали 5–6 месяцев в году, а в остальное время Рачинский индивидуально занимался с детьми постарше, готовя их к поступлению в различные учебные заведения следующей ступени; начальная народная школа не была прямо связана с другими учебными заведениями и после нее нельзя было продолжить обучение без добавочной подготовки. Рачинский желал видеть наиболее продвинутых из своих учеников учителями начальной школы и священниками, так что готовил он детей преимущественно в духовные и учительские семинарии. Бывали и значительные исключения — прежде всего, это сам автор картины, Николай Богданов–Бельский, которому Рачинский помог попасть в Московское училище живописи, ваяния и зодчества. Но, как ни странно, вести крестьянских детей по магистральному пути образованного человека — гимназия / университет / государственная служба — Рачинский не желал.
Рачинский писал популярные педагогические статьи и продолжал пользоваться определенным влиянием в столичных интеллектуальных кругах. Наиболее важным оказалось знакомство с ультравлиятельным Победоносцевым. Под определенным влиянием идей Рачинского духовное ведомство решило, что от земской школы толку не будет — либералы детей хорошему не научат — и в середине 1890–х начало развивать собственную независимую сеть церковно–приходских школ.
Кое в чем церковно–приходские школы были похоже на школу Рачинского — в них было много церковно–славянского языка и молитв, а остальные предметы были соответственно сокращены. Но, увы, им не передались достоинства Татевской школы. Священники школьным делом интересовались мало, управляли школами из–под палки, сами в этих школах не преподавали, а учителей наняли самых третьесортных, и платили им заметно меньше, чем в земских школах. Крестьяне церковно–приходскую школу невзлюбили, так как поняли, что полезному там почти не учат, молитвы же их интересовали мало. Кстати, именно учителя церковной школы, набранные из парий духовного сословия, оказались одной из самых революционизированных профессиональных групп того времени, и именно через них в деревню активно проникала социалистическая пропаганда.
Теперь мы видим, что это обычное дело — любая авторская педагогика, рассчитанная на глубокую вовлеченность и энтузиазм учителя, немедленно дохнет при массовом воспроизведении, попадая в руки незаинтересованных и вялых людей. Но для того времени это был большой облом. Церковно–приходские школы, к 1900 году составлявшие около трети начальных народных школ, оказались немилы всем. Когда, начиная с 1907 года, государство стало направлять в начальное образование большие деньги, не было и речи о том, чтобы провести через Думу субсидии церковным школам, почти все средства ушли земцам.
Более распространенная земская школа достаточно сильно отличалась от школы Рачинского. Для начала, земцы считали Закон Божий совершенно бесполезным. Отказаться от его преподавания было нельзя, по политическим причинам, поэтому земства как могли задвинули его в угол. Закону Божьему учил приходской священник, которому платили мало и не обращали на него внимания, с соответствующими результатами.
Математике в земской школе учили хуже, чем у Рачинского, и в меньшем объеме. Курс оканчивался на операциях с простыми дробями и неметрической системе мер. До возведения в степень обучение не доходило, так что ученики обыкновенной начальной школы просто не поняли бы задачу, изображенную на картине.
Обучение русскому языку земская школа пыталась превратить в мироведение, через так называемое объяснительное чтение. Методика состояла в том, что диктуя учебный текст по русскому языку, учитель также и дополнительно пояснял школьникам, о чем говорится в самом тексте. Таким паллиативным образом уроки русского языка превращались также в географию, природоведение, историю — то есть во все те развивающие предметы, которым не нашлось места в коротком курсе одноклассной школы.
Итак, наша картина изображает не типичную, а уникальную школу. Это памятник Сергею Рачинскому, уникальной личности и педагогу, последнему представителю той когорты консерваторов и патриотов, к которой еще нельзя было отнести известное выражение "патриотизм — последнее прибежище негодяя". Массовая народная школа была в хозяйственном отношении обустроена значительно беднее, курс математики в ней был короче и проще, а преподавание слабее. И, конечно же, ученики обыкновенной начальной школы не могли не только решить, но и понять задачу, воспроизведенную на картине.
Кстати, а каким методом школьники решают задачу на доске? Только прямым, в лоб: умножить 10 на 10, запомнить результат, умножить 11 на 11, сложить оба результата, и так далее. Рачинский считал, что у крестьянина не бывает под рукой письменных принадлежностей, поэтому он учил только устным приемам счета, опуская вся арифметические и алгебраические преобразования, требующие вычисления на бумаге.
отсюда




101.livejournal.com
Урок-экскурсия по картине Н.П. Богданова-Бельского "Устный счет"

Разделы: Математика, МХК и ИЗО
Цели урока:
- развитие способностей наблюдать;
- развитие способностей мыслить;
- развитие способностей выражать мысль;
- привитие интереса к математике;
- прикосновение к искусству Н.П. Богданова-Бельского.
ХОД УРОКА
Ученье – труд, который воспитывает и формирует человека.
Четыре страницы из жизни картины
Страница первая
Картина “Устный счет” была написана 1895 году, то есть 110 лет назад. Это своеобразный юбилей картины, которая является творением рук человека. Что изображено на картине? Какие-то мальчики собрались около классной доски, и что-то рассматривают. Два мальчика (это те, которые стоят впереди) отвернулись от доски и что-то вспоминают, а, может быть, считают. Один мальчик что-то шепчет на ухо человеку, по-видимому, учителю, а другой, кажется, подслушивает.
– А почему они в лаптях?
– А почему тут нет девочек, только одни мальчики?
– А почему они стоят спиной к учителю?
– А что они делают?
Вы уже, верно, поняли, что здесь изображены учащиеся и учитель. Конечно, костюмы учащихся необычные: некоторые ребята в лаптях, а у одного из героев картины (того, который изображен на переднем плане), кроме того, и рубаха порвана. Ясно, что эта картина не из нашей школьной жизни. Вот и надпись на картине 1895 год – время старой дореволюционной школы. Крестьяне жили тогда бедно, сами они и их дети ходили в лаптях. Художник изобразил здесь крестьянских детей. Только в то время мало кто из них мог учиться даже в начальной школе. Посмотрите-ка на картину: ведь только трое из учеников в лаптях, а остальные – в сапогах. Очевидно, ребята из семей богатых. Ну, а почему на картине не изображены девочки, это тоже нетрудно понять: ведь в то время девочек, как правило, в школу не принимали. Ученье было “не их делом”, да и мальчики-то учились далеко не все.
Страница вторая
Эта картина называется “Устный счет”. Посмотрите, как сосредоточенно думает мальчик, изображенный на переднем плане картины. Видно нелегкую задачу дал учитель. Но, наверное, этот ученик уже скоро закончит свою работу, а ошибки не должно быть: уж очень серьезно относится он к устному счету. А вот тот ученик, который что-то шепчет на ухо учителю, видно, уже решил задачу, только ответ его не совсем правильный. Смотрите: учитель слушает ответ ученика внимательно, но на лице его нет одобрения, значит, ученик сделал что-то не так. А может быть, учитель терпеливо ожидает, когда и другие сосчитают верно, так же как первый и поэтому не спешит одобрить его ответ?
– Нет, первый даст правильный ответ, тот который стоит впереди: сразу видно, что он лучший ученик в классе.
А какую же задачу дал им учитель? Не сможем ли решить ее и мы?
– А вот попробуйте.
На доске я запишу так, как привыкли писать вы:
(10·10+11·11+12·12+13·13+14·14):365
Как видно, каждое из чисел 10, 11, 12, 13 и 14 нужно умножить само на себя, результаты сложить, а полученную сумму разделить на 365.
– Вот так задача (такой пример не скоро решишь, да еще в уме). А все-таки попробуйте сосчитать устно, в трудных местах я буду помогать вам. Десятью десять – 100, это каждый знает. Одиннадцать умножить на одиннадцать – это тоже нетрудно сосчитать: 11·10=110, да еще 11 – всего 121. 12·12 – это тоже не хитро сосчитать: 12·10=120, да еще 12·2=24, а всего будет 144. Так же я сосчитал, что 13·13=169 и 14·14=196.
Но пока я умножал, то почти забыл, какие числа у меня получились. Потом я вспомнил их, а ведь эти числа надо еще сложить, да потом сумму разделить на 365. Нет, это уже сами вы не сможете вычислить.
– Придется немного помочь.
– Какие же числа у вас получились?
– 100, 121, 144, 169 и 196 – это сосчитали многие.
– Теперь вы, наверное, хотите сложить сразу все пять чисел, а потом уже делить результаты на 365?
– Мы это сделаем по-другому.
– Ну-ка, сложим первые три числа: 100, 121, 144. Сколько получится?
– 365.
– А делить на сколько надо?
– Тоже на 365!
– Сколько же получится, если сумму первых трех чисел разделить на 365?
– Один! – это уже каждый сообразит.
– Теперь сложите остальные два числа: 169 и 196. Сколько получится?
– Тоже 365!
– Вот так пример, и совсем нехитрый. Получается-то всего лишь два!
– Только для его решения надо хорошо знать, что сумму можно делить не сразу всю, а по частям каждое слагаемое в отдельности, или же по группам в два-три слагаемых, а потом уж сложить получившиеся результаты.
Страница третья
Эта картина называется “Устный счет”. Написал ее художник Николай Петрович Богданов-Бельский, который жил с 1868 по 1945 год.
Богданов-Бельский очень хорошо знал своих маленьких героев: вырос в их среде, был когда-то пастушком. “…Я незаконнорожденный сын бедной бобылки, оттого Богданов, а Бельский стал по имени уезда”, - рассказывал художник о себе.
Ему посчастливилось попасть в школу известного русского педагога профессора С.А. Рачинского, который заметил художественный талант мальчика и помог ему получить художественное образование.
Н.П. Богданов-Бельский окончил Московское училище живописи, ваяния и зодчества, учился у таких известных художников, как В.Д. Поленов, В.Е. Маковский.
Немало портретов и пейзажей написано Богдановым-Бельским, но в памяти людей он остался, прежде всего, как художник, сумевший поэтично и верно рассказать о смышленой сельской детворе, жадно тянувшейся к знаниям.
Кому из нас не знакомы картины “У дверей школы”, “Новички”, “Сочинение”, “Деревенские друзья”, “У больного учителя”, “Проба голоса”, - вот название лишь некоторых из них. Чаще всего художник изображает детей в школе. Прелестные, доверчивые, сосредоточенные, задумчивые, полные живого интереса и всегда отмеченные природным умом – такими знал и любил крестьянских ребятишек Богданов-Бельский, такими увековечил в своих произведениях.
Страница четвертая
Художник изобразил на этой картине невыдуманных учеников и учителя. С 1833 по 1902 год жил известный русский педагог Сергей Александрович Рачинский, замечательный представитель русских образованных людей позапрошлого века. Он был доктором естественных наук и профессором ботаники Московского университета. В 1868 году С.А. Рачинский решается идти в народ. “Он держит экзамен” на звание учителя начальных классов. На свои средства открывает школу для крестьянских детей в селе Татьево Смоленской губернии и становится в ней учителем. Так вот, его ученики так хорошо считали устно, что этому удивлялись все посетители школы. Как видите, художник изобразил С.А. Рачинского вместе с его учениками на уроке устного решения задач. Между прочим, сам художник Н.П. Богданов-Бельский был учеником С.А. Рачинского.
Это картина – гимн учителю и ученику.
xn--i1abbnckbmcl9fb.xn--p1ai
Проект "Экскурсия по картине Богданова-Бельского "Устный счет""
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СОШ №1» Г.ЖИЗДРЫ КАЛУЖСКОЙ ОБЛАСТИ
ПРОЕКТ
Экскурсия по картине Богданова-Бельского «Устный счёт»
Автор: Богданов Ярослав,
учащийся 5а класса
Руководитель: Яшина Н.М.,
учитель математики
г. Жиздра
2014
Содержание:
Пояснительная записка---------------------------------------------------- 3
Введение --------------------------------------------------------------------- 4
Основная часть-------------------------------------------------------------- 5
Страница первая. Рассказ об изображении на картине.------ 5
Страница вторая. Как решить пример устно. ------------------ 7
Страница третья. Рассказ о художнике.-------------------------- 8
Страница четвертая. Знакомство с учителем, Сергеем Александровичем Рачинским.--------------------------------------- 9
Заключение------------------------------------------------------------------ 10
Литература----------------------------------------------------------------- 11
Приложение1
В Третьяковской галерее------------------------------------------------ 12
Приложение 2.
Неизвестный для меня способ решения------------------------------ 13
Приложение 3.
ТАБЛИЦА КВАДРАТОВ ЧИСЕЛ ОТ 10 ДО 20----------------------- 14
Пояснительная записка
Мне нравится предмет математика. Мне нравится считать, решать примеры, задачи. Особенно я радуюсь, когда решу правильно трудный пример или сложную задачу.
В этом году мы изучали тему «Степень». Когда я увидел пример на картине, подумал, что его трудно решить. Но картина называется «Устный счет». Значит, его надо решить устно. Я заинтересовался и примером, и картиной. Так я выбрал тему своего проекта. Она называется «Экскурсия по картине Н.П.Богданова – Бельского «Устный счёт»».
Цель проекта:
Изучить картину Н.П.Богданова-Бельского «Устный счёт» и составить по ней экскурсию.
Задачи:
Решить пример, написанный на картине,
Узнать информацию об авторе Н.П.Богданове-Бельском,
создать мультимедийную презентацию о проекте,
Создать таблицу квадратов для чисел от 10 до 20.
Гипотеза: я предположил, что решив пример письменно, я найду способ, чтобы решить его устно. Я начал решение с повторения темы «Степень». Затем я составил таблицу квадратов необходимых чисел, чтобы можно было легче решить пример. Внимательно рассмотрев картину, я понял, что дети считают устно, без помощи таблицы. Мне стало интересно изучать картину всю, до мельчайших подробностей. В книгах, а также в интернете я стал искать сведения о картине и ее авторе, художнике Н.П.Богданове-Бельском.
Таким образом, я составил экскурсию об этой картине и рассказ о художнике, а также учителе, который изображен на ней. Вместе с учителем я разобрался в примере. Я понял, что пример можно, если постараться, решить устно. Моя гипотеза подтвердилась.
В ходе выполнения проекта я решил поставленные задачи. Я составил экскурсию по картине. Она состоит из четырех страниц. Первая страница рассказывает, что изображено на картине. Вторая - учит, как решить пример устно. Третья знакомит нас с художником, а четвертая с учителем, Сергеем Александровичем Рачинским. Задачи Рачинского встречаются и в нашем учебнике математики.
Эта картина – гимн учителю и ученику.
Мне удалось достигнуть поставленной цели. Мне очень приятно, что я сделал этот проект.
В интернете я нашел другие способы решения этого примера, но пока мне не хватает знаний, чтобы понять их.
Литература: Математика №3(15)/2007, «Устный счет», М., Чистые пруды, 2007.
Введение
Мне нравится предмет математика. Мне нравится считать, решать примеры, задачи. Особенно я радуюсь, когда решу правильно трудный пример или сложную задачу.
В этом году мы изучали тему «Степень». Когда я увидел пример на картине, подумал, что его трудно решить. Но картина называется «Устный счет». Значит, его надо решить устно. Я заинтересовался и примером, и картиной. Так я выбрал тему своего проекта. Она называется «Экскурсия по картине Н.П.Богданова – Бельского «Устный счёт»».
Цель проекта:
Изучить картину Н.П.Богданова-Бельского «Устный счёт» и составить по ней экскурсию.
Задачи:
Решить пример, написанный на картине,
Узнать информацию об авторе Н.П.Богданове-Бельском,
создать мультимедийную презентацию о проекте,
Создать таблицу квадратов для чисел от 10 до 20.
Гипотеза: я предположил, что решив пример письменно, я найду способ, чтобы решить его устно. Я начал решение с повторения темы «Степень». Затем я составил таблицу квадратов необходимых чисел, чтобы можно было легче решить пример. Внимательно рассмотрев картину, я понял, что дети считают устно, без помощи таблицы. Мне стало интересно изучать картину всю, до мельчайших подробностей. В книгах, а также в интернете я стал искать сведения о картине и ее авторе, художнике Н.П.Богданове-Бельском.
Основная часть
Я решил составить экскурсию об этой картине и рассказ о художнике, а также учителе, который изображен на ней. Вместе с учителем я разобрался в примере. Я понял, что пример можно, если постараться, решить устно. Моя гипотеза подтвердилась.
СТРАНИЦА ПЕРВАЯ
Картина «Устный счёт» была написана в 1895 г., то есть почти 120 лет назад.
Что изображено на картине? Мальчики собрались около классной доски и что-то рассматривают. Два мальчика(стоят впереди),отвернулись от доски и что-то вспоминают, а может быть считают. Один что-то шепчет на ухо человеку, по-видимому учителю, а другой, кажется, подслушивает.
- А почему они в лаптях?
- А почему тут нет девочек, только одни мальчишки?
- А почему они стоят спиной к учителю?
- А что они делают?
Вы уже, Верно поняли что здесь изображены учащиеся и учитель. Конечно, костюмы учащихся необычные: некоторые ребята в лаптях, а у одного из героев картины (того, который изображён на переднем плане) и рубаха порвана. Ясно, что это картина не из нашей школьной жизни. Вот и надпись на картине: 1895 год - время старой дореволюционной школы. Крестьяне жили тогда бедно, сами они и их дети ходили в лаптях. В то время мало кто из них мог учиться даже в начальной школе. Посмотрите-ка на картину: ведь только трое из учащихся в лаптях, а остальные – в сапогах. Очевидно, ребята из богатых семей. Ну, а почему на картине не изображены девочки, это тоже нетрудно понять: в то время девочек, как правило, в школу не принимали. Учение было «не их делом», да и мальчики-то учились далеко не все

СТРАНИЦА ВТОРАЯ
Эта картина называется «Устный счет». Посмотрите, как сосредоточенно думает мальчик, изображенный на переднем плане. Видно, не легкую задачу дал учитель. Но этот ученик, наверное, скоро закончит работу, ошибки не должно быть: уж очень серьезно относится он к устному счету. А тот, который что-то шепчет на ухо учителю, кажется, уже решил задачу, только его ответ не совсем правильный. Смотрите: учитель слушает ученика внимательно, но в лице нет одобрения, значит, ученик сделал что-то не так. А может, учитель терпеливо ожидает, когда и другие сосчитают, а потому не спешит одобрять его ответ?
- Нет, первым даст правильный ответ тот, кто стоит впереди: сразу видно, что он лучший ученик в классе.
Какую же задачу дал им учитель? Не сможем ли решить ее и мы?
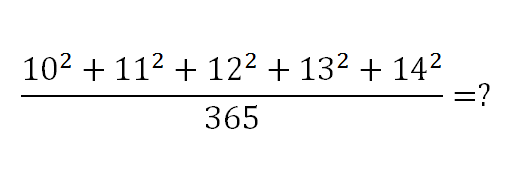
(10·10+11·11+12·12+13·13+14·14):365
Как видно, каждое из чисел 10,11,12,13 и 14 нужно умножить само на себя, результаты сложить, а полученную сумму разделить на 365.
-Вот так задача! Такой пример не скоро решить, да ещё в уме.
А всё-таки, попробуйте сосчитать устно, в трудный местах я буду помогать вам. Десятью десять - сто, это каждый знает. Одиннадцать умножить на одиннадцать – это тоже не трудно сосчитать:10·11=110 да ещё 11, всего 121. Умножая 12 на 12, поступаем так: 12·10=120, да ещё 12·2=24, а всего будет 144.
Действуя аналогично, получите 13·13=169 и 14·14=196.
Но пока мы умножали, то почти забыли, какие числа получились ранее. Потом вспомню их, а ведь эти числа надо ещё и сложить, да потом сумму разделить на 365. Придётся вам немного помочь. Какие числа у вас получились?
-100, 121, 144, 169, 196.
Теперь вы, наверное, хотите сложить сразу все пять чисел и разделить их на 365.Давайте вы это сделаем по -другому. Давайте сложим первые три числа 100, 121, 144. Сколько получится?
-365
Теперь сложим остальные два числа: 169 и 196. Сколько получится?
-Тоже 365!
- Вот так пример, и совсем нехитрый. Получается-то всего лишь два! Только для его решения надо хорошо знать, что сумму можно делить не сразу всю, а каждое слагаемое в отдельности или же по группам в два-три слагаемых, а потом уж сложить получившиеся результаты.
СТРАНИЦЫ ТРЕТЬЯ
Картина называется «Устный счёт». Написал ее художник Николай Петрович Богданов-Бельский (1868-1945).
Богданов-Бельский очень хорошо знал своих маленьких героев: вырос в их среде, был когда-то пастушком. «Я незаконнорождённый сын бедной бобылки, оттого Богданов, а Бельским стал по имени уезда»,- рассказывал художник о себе.
Ему посчастливилось попасть в школу известного русского педагога профессора C.A. Рачинского, который заметил художественный талант мальчика и помог ему получить художественное образование.
Н.П. Богданов-Бельский окончил Московское училище живописи, ваяния и зодчества, учился у таких известных художников как B.Д. Поленов, В.E. Маковский.
Немало портретов и пейзажей написано Богдановым-Бельским, но в памяти людей он остался, прежде всего, как художник, сумевший поэтично и верно поведать о смышлёной сельской детворе, жадно тянувшейся к знаниям.
« У дверей школы», «Новички», «Сочинение», «Деревенские друзья», «У больного учителя», «Пробы голоса»- вот названия лишь некоторых из его картин. На них чаще всего художник изображал детей в школе. Прелестные, Доверчивые, сосредоточенные, задумчивые, полные живого интереса и всегда отмеченные природным умом- такими знал и любил крестьянских детишек Богданов-Бельский, такими увековечил их в своих произведениях.
СТРАНИЦА ЧЕТВЕРТАЯ
Художник изобразил на этой картине невыдуманных учеников и учителя. Учитель- это Сергей Александрович Рачинский, известный русский педагог, замечательный представитель русских образованных людей позапрошлого века. Он был доктором естественных наук и профессором ботаники Московского университета. В 1868 году С.А Рачинский решает «уйти в народ». Он держит экзамен на звание учителя начальных классов. На свои средства открывает школу для крестьянских детей в селе Татево Смоленской губернии и становится в ней учителем. Его Ученики так хорошо считали устно, что этому удивлялись все посетители школы. Не случайно, художник изобразил C.A. Рачинского вместе с его учениками именно на уроке устного решения задач.
ЭТА КАРТИНА- ГИМН УЧИТЕЛЮ И УЧЕНИКУ!
Заключение
В ходе выполнения проекта я решил поставленные задачи. Я составил экскурсию по картине. Она состоит из четырех страниц. Первая страница рассказывает, что изображено на картине. Вторая - учит, как решить пример устно. Третья знакомит нас с художником, а четвертая с учителем, Сергеем Александровичем Рачинским. Задачи Рачинского встречаются и в нашем учебнике математики.
Эта картина – гимн учителю и ученику.
Мне удалось достигнуть поставленной цели. Я решил пример устным способом.
Продуктом моей работы стали: мультимедийная презентация, реферат, создание справочной таблицы-буклета «Таблица квадратов чисел от10 до 20».
Мне очень приятно, что я сделал этот проект.
В интернете я нашел другие способы решения этого примера, но пока мне не хватает знаний, чтобы понять их.
Литература:
Математика №3(15)/2007, «Устный счет», М., Чистые пруды, 2007.
Википедия, статьи.
Приложение 1.
В Третьяковской галерее

Приложение 2.
Неизвестный для меня способ решения
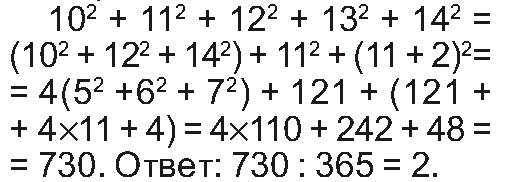
Приложение 3.
ТАБЛИЦА КВАДРАТОВ ЧИСЕЛ ОТ 10 ДО 20
102
10·10
100
112
11·11
121
122
12·12
144
132
13·13
169
142
14·14
196
152
15·15
225
162
16·16
256
172
17·17
289
182
18·18
324
192
19·19
361
202
20·20
400
ТАБЛИЦА КВАДРАТОВ ЧИСЕЛ ОТ 10 ДО 20
102
10·10
100
112
11·11
121
122
12·12
144
132
13·13
169
142
14·14
196
152
15·15
225
162
16·16
256
172
17·17
289
182
18·18
324
192
19·19
361
202
20·20
400
infourok.ru
Задачи-обобщения по картине "Устный счет" |

В одной из недавних статей мы рассматривали несоизмеримый вклад в образование императорской России такой легендарной личности как Сергей Александрович Рачинский. Именно он изображен на известной картине русского художника Николая Богданова-Бельського “Устный счет. В народной школе С.А.Рачинского”.
Главный герой картины- это… математический пример, который сам Рачинский , будучи преподавателем сельской школы, изображенной на картине, преподнес для своих учащихся.

По поводу этого примера Рачинский говорил так:
«Эта задача ещё и тем хороша, что она не только мозг оттачивает, но и для многих, далеко идущих, обобщений годна»
Но таких примеров, как говорит история математики, у Рачинского в запасе было не один десяток. Об этом его книги , в которых собраны задачи по математике на тему “Устный счет”:
А вот обобщение известной задачи Рачинского с картины Богданова-Бельського “Устный счет”, мы и рассмотрим в данной статье.
Задача 1. Найти пять последовательных натуральных чисел таких, что сумма первых трех равна сумме двух последующих.
Ответ: числа 4, 5, 6, 7, 8. Пусть х- наибольшее число первой суммы; составим уравнение: (х-2) + (х-1) + х = (х + 1) + (х + 2).После упрощения получим х= 6.
Задача 2 . Найти семь последовательных натуральных чисел таких, что сумма первых четырех равна сумме трех последующих.
Ответ: числа 9,10, 11,12, 13, 14 и 15. Решение аналогично задаче № 1. х = 12.
Задача 3. Найти три последовательных натуральных числа таких, что сумма квадратов первых двух чисел была равна квадрату третьего числа. Сколько решений имеет задача?
Ответ: числа 3, 4, 5. Пусть х- большее из первых двух чисел, тогда по условию, имеем : (х – 1) ^2 + х^ 2 = (х + 1) ^2 Тогда: Х =0, х=4. Искомые числа: -1, 0, 1 и 3, 4, 5.
Задача 4. Найти пять последовательных натуральных чисел таких, что сумма квадратов первых трех чисел равна сумме квадратов двух последующих чисел.
Ответ: 10, 11, 12, 13, 14. Задача имеет единственное решение в натуральных числах .
Пусть х- наибольшее число первой суммы; тогда (х-2)^ 2 + (х – 1) ^2 + х ^2 = (х + 1)^ 2 + (х+2) ^2 , откуда х (х – 12)=0, х=0 и х=12. Поскольку в условии задачи говорится о натуральных числах, то получим числа 10, 11, 12, 13, 14. Именно эти числа и использованы в рассматриваемой в данной статье картине « Устный счет » .
Задача 5. Существует ли решение задачи для девяти последовательных натуральных чисел?
Ответ: Существует. Числа 36, 37, 38, 39, 40, 41, 42, 43, 44. Решение аналогично решению задач №3, №4.
Задача 6. Найти решение Задачи №3 для третьих степеней. .
Ответ: Решения в натуральных числах нет. После упрощения получим х^ 3 – 6х^ 2 -2=0; х^ 2 (х-6)=2; для того, чтобы левая часть была положительной, наименьшее натуральное х=7, тогда 49 *1=2, с ростом х неравенство усиливается, натуральных решений нет.
Задача 7 . Найти решение Задачи# 4 для третьих степеней.
Ответ: Решения в натуральных числах нет.
Можно так же привести примеры из задачника самого С.А.Рачинского «1001 задача для устного счета». Но это уже тема другой статьи.
Ну как? Сильные задачки ?
Передайте, пожалуйста, нажав кнопочки ниже, другим читателям эту информацию. Пусть и они владеют тем, о чем узнали только что вы.
repetitor-problem.net
Решение задачи Рачинского | Блог 4brain
На картине Николая Петровича Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского», написанной в 1895 году, сельские школьники решают очень интересный пример. Видно, что им он дается непросто. Похоже, только один парень из одиннадцати одноклассников догадался, как решать этот пример в уме.

А вы сможете посчитать в уме, чему равняется это выражение?
Решение
Первый способ решения
Для того, чтобы решить это выражение существует несколько способов. Если вы в школе учили квадраты чисел до 20 или до 25, то скорее всего она не вызовет у вас особого труда. Это выражение равно: (100+121+144+169+196) разделить на 365, что в итоге преобразовывается в частное 730 и 365, что равняется: 2. Чтобы решить пример этим способом вам могут пригодиться навыки внимательности и умение держать в уме несколько промежуточных ответов. Как развить эти навыки смотрите в первом нашем уроке устного счета.
Второй способ решения
Если вы в школе не учили значения квадратов чисел до 20, то вам может пригодиться простой способ, основанный на применении опорного числа. Этот способ позволяет просто и быстро перемножать два любых числа, меньшие 20, и подробно описан в уроке 4. Способ очень прост, нужно к первому числу прибавить единицу второго, умножить эту сумму на 10, а затем прибавить произведение единиц. Например: 11*11=(11+1)*10+1*1=121. Остальные квадраты находятся также:
- 12*12=(12+2)*10+2*2=140+4=144
- 13*13=160+9=169
- 14*14=180+16=196
Затем, найдя все квадраты, задание можно решить так же, как показано в первом способе.
Третий способ решения
Еще один способ предполагает использовать упрощение числителя дроби, основанное на использовании формул квадрата суммы и квадрата разности (которые подробно описаны в уроке по возведению в квадрат в уме). Если попытаться выразить квадраты в числителе дроби через число 12, то получим следующее выражение. (12 — 2)2 + (12 — 1)2 + 122 + (12 + 1)2 + (12 + 2)2 . Если вы хорошо знаете формулы квадрата суммы и квадрата разности, то вы поймете, как это выражение легко привести к виду: 5*122+2*22+2*12, что равняется 5*144+10=730. Чтобы 144 умножить на 5 достаточно просто поделить это число на 2 и умножить на 10, что равняется 720 (эта и другие простейшие арифметические закономерности описаны во втором уроке). Потом это выражение делим на 365 и получаем: 2.
Четвертый способ решения
Также эту задачу можно решить за 1 секунду, если вы знаете последовательности Рачинского, о которых вы можете прочитать на данной странице.
4brain.ru
Устный счет в "безграмотной России"
Знаменитый русский художник Николай Петрович Богданов-Бельский написал уникальную и невероятно жизненную историю в 1895 году. Произведение называется «Устный счёт», а в полной версии «Устный счёт. В народной школе С.А.Рачинского».
Вот у меня вопрос, вы сможете в уме решить задачку, которая написана на доске?
Вот вам поближе это математическое выражение:
Давайте прежде чем узнать ответ, честно ответив в опросе, смогли ли вы устно это решить или нет. Я вот не смог. А вы?
Смогли ли вы устно решить это выражение?
Да, я решил
456(71.5%)
Нет, у меня не получилось
182(28.5%)
А теперь немного подробнее про эту картину и конечно же результат выражения ...
Картина написана маслом по холсту, на ней изображена сельская школа 19 века во время урока арифметики. Школьники решают интересный и сложный пример. Они находятся в глубокой задумчивости и поиске верного решения. Кто-то думает у доски, кто-то стоит в сторонке и пытается сопоставить знания, которые помогут при решении задачи. Дети полностью поглощены поиском ответа на поставленный вопрос, они хотят доказать себе и миру, что могут это сделать.
Рядом стоит учитель, прототипом которого является сам Рачинский – знаменитый ботаник и математик. Не зря картине присвоено такое название, оно в честь профессора Московского университета. На полотне изображено 11 человек детей и только один мальчик тихо шепчет учителю на ухо, возможно правильный ответ.
На картине изображён простой русский класс, дети одеты в крестьянскую одежду: лапти, штаны и рубахи. Всё это очень гармонично и лаконично вписывается в сюжет, ненавязчиво неся миру тягу к знаниям со стороны простого русского народа.
Тёплая цветовая гамма несёт доброту и простоту русского народа, здесь нет зависти и фальши, нет зла и ненависти, дети из разных семей с разным достатком собрались воедино для принятия единственно верного решения. Этого очень не хватает в нашей современной жизни, где люди привыкли жить совсем по – другому, не считаясь, с мнением окружающих.
Николай Петрович посвятил картину своему учителю, великому гению математики, которого хорошо знал и уважал. Сейчас картина находится в Москве в Третьяковской галерее, будете там, обязательно взгляните на перо великого мастера.
Так, в уме я конечно считать не буду, потому что не смогу, а вот что получается на калькуляторе:
100+121+144+169+196 / 365 = 2
Вот такая вот интересная картина ...
Вот так, кстати, уже позже по стране двигался ЛИКБЕЗ, а вот уровень математической подготовки во Франции
masterok.livejournal.com
Устный счёт | Твиттергуру
Устный счёт
 11 июля 2014
11 июля 2014  mb59
mb59 
Вчера попалась на глаза картина Богданова-Бельского «Устный счёт». Она написана в 1895 году. Там детишки в народной школе Рачинского пытаются в уме решить довольно сложный арифметический пример. Или даже алгебраический — возведение в квадрат — это уже не простая арифметика, не так ли?

Решил увеличить изображение и посмотреть, чем же так озадачил детвору похожий на Бориса Пастернака педагог.

Или в текстовом формате
 Я уже не помню, существуют ли какие-то способы быстрого сложения квадратов, поэтому просто возвёл все пять чисел и последовательно суммировал. Без бумажки и калькулятора действительно непросто, но я справился. Как вы думаете, что у меня получилось? Ну разумеется! Знаменитая картина Решетникова!
Я уже не помню, существуют ли какие-то способы быстрого сложения квадратов, поэтому просто возвёл все пять чисел и последовательно суммировал. Без бумажки и калькулятора действительно непросто, но я справился. Как вы думаете, что у меня получилось? Ну разумеется! Знаменитая картина Решетникова!

Результат примера — 2.
На картине «Устный счёт» пацанам лет от 8 до 15. Ну, или они так выглядят, а на самом деле постарше. Это сейчас кругом акселераты. Думаю вот, а нынешние школьники такую задачу решат? Без технических средств — только собственным умом?
Напоследок немного юмора в тему.


© mb59
Комментарии и уведомления в настоящее время закрыты..twitterguru.ru










