Натуральные числа. Некоторые числовые закономерности. Картина трудная задача
Натуральные числа. Некоторые числовые закономерности

Разделы: Математика
Тема: Натуральные числа. Некоторые числовые закономерности ( приёмы быстрого счёта).
Цель:
- Познакомить учащихся с числовыми закономерностями.
- Учить обобщению и выводу общих закономерностей, связанных с рядом натуральных чисел.
- Познакомить с историческими сведениями, связанными с развитием математической науки.
- Развивать интерес к предмету, связывая его с литературой, искусством, учить видеть красоту натуральных чисел.
Оборудование урока:
- Репродукции И.Е. Репина, В.И. Сурикова, И. И.Шишкина, В.М.Васнецова, И. И. Левитана и других.
- Картина художника Богданова – Бельского «Трудная задача» (Рисунок 1)
- Для каждого ученика карта – задание на урок (Приложение 1)
Ход урока:
- Сегодня на уроке мы познакомимся с числовыми закономерностями, о некоторых мы вскользь уже говорили на предыдущих уроках, с некоторыми мы встретимся впервые.
Итак, пусть это вас не удивляет, но я предлагаю путешествие по картинной галерее.
- В наш маленький городок прибыла выставка работ художников - передвижников. И я вас приглашаю на экскурсию в картинную галерею. Общество художников - передвижников образовалось в 1870 г., членами этого общества были И.Е. Репин, В.И. Суриков, И. И.Шишкин, В.М.Васнецов, И. И. Левитан и др. Они правдиво изображали жизнь и историю народа, родную природу, обличали порядки самодержавной России.
В зале вы видите картины художников Маковецкого "Свидание", "За лекарством".
- Следующая картина русского живописца конца XIX начала XX века Николая Петровича Богданова-Бельского (1868 - 1945 гг.). Он писал жанровые картины, посвященные сельской школе, крестьянским детям. Наиболее известна его картина "Трудная задача", написанная в 1895 году. К сожалению, вы видите маленькую копию этой картины (Приложение 1). Чтобы всем было хорошо её видно, мы вам это покажем. (Ребята в образе как изображено на картине, в таких же костюмах и с тем же выражением лиц замирают).
- Далеко не в центре вы видите педагога С. А Рачинского. На картине он изображен с сохранением портретного сходства. С. А Рачинский - педагог, профессор естественных наук, покинувший университетскую кафедру, чтобы сделаться рядовым учителем сельской школы. Талантливый педагог культивировал в своей школе устный счет, основанный на виртуозном использовании свойств чисел.
- Многие помнят эту картину, но немногие из тех, кто видел её в Третьяковке или на репродукциях или, глядя на картину сейчас, обращали внимание на содержание самой математической задачи, написанной мелом на доске.
- А задача действительно не из легких. Судите сами! Состоит она в том, чтобы устным счетом быстро найти результат.
Задача 1.
Ученики Рачинского хорошо справлялись с подобными задачами. По выражению лица педагога видно, что некоторые ученики уже сказали ему правильный ответ. Только новички ещё испытывают затруднения. Но и они вот-вот найдут правильное решение.
- Итак, спустя 100 лет, сможем ли мы решить эту "трудную задачу"?
Числа 10, 11, 12, 13, 14 обладают удивительной любопытной особенностью: на прошлом уроке мы повторяли квадраты этих и других чисел, 102 +112+122 = 132 + 142
А так как 100 + 121 + 144 равно 365, 132 + 142 тоже 365, то легко рассчитать в уме, что воспроизведенное на картине выражение равно 2.
(так как дробная черта - это знак деления)
- 365 - удивительное число еще и тем, что определяет число дней в году, а при делении на 7 дает в остатке 1, что имеет значение для старого семидневного календаря.
- Прекрасно, мы справились с задачей С. А Рачинского. Но в математике существует достаточное количество цифровых и числовых диковинок, которые на вид трудно считаются даже не устно.
Посчитаем сумму чисел от 1 до 20, это можно сделать всего секунд за десять, записывать эту сумму совершенно не обязательно. Самое главное в способе подсчета.
Задача 2
А теперь решим задачу Гаусса.
- Немецкого ученого Карла Гаусса называли королем математиков. Его математическое дарование проявилось ещё в детстве. Рассказывают, что в трехлетнем возрасте он удавил окружающих, поправив расчеты своего отца с каменщиками. Однажды в школе (Гауссу в то время было 10 лет) учитель предложил классу сложить все числа от 1 до 100. Пока он диктовал задание, у Гаусса уже был готов ответ. А у вас? На грифельной доске у него было написано 101·50 = 5050.
| Посчитать сумму чисел от и до | Чисел |
Пар |
Сумма крайних |
Результат |
| От 1 до 20 | 20 |
10 |
21 |
210 |
| От 1 до 100 | 100 |
50 |
101 |
5050 |
| От 1 до 50 | 50 |
25 |
51 |
1275 |
| От 1 до 30 | 30 |
15 |
31 |
465 |
| От 1 до n | n |
n/2 |
n +1 |
n ( n+1)/2 |
| От 101 до 300 | 200 |
100 |
401 |
40100 |
| От 51 до 450 | 400 |
200 |
501 |
100200 |
Мы автоматически вывели формулу для вычисления суммы n чисел, чисел было чётное количество, а для нечетного n эта формула справедлива?
(Формула верна для любого n).
Но докажем немного по-другому, ведь нечетное число чисел не разобьешь на пары. Поступим так, запишем искомую сумму дважды 1 + 2 + … + (n - 1) + n.
n + (n – 1) + … + 2 + 1
Сумма пар (n + 1), пар всего n штук значит, нашу двойную сумму можно посчитать так n·(n +1) так как слагаемые от 1 до n мы сложили дважды, то полученную сумму мы разделим на 2. Получилась та же формула
- Для чего нужна эта формула? ( Для быстрого вычисления суммы)
В "трудной задаче" Рачинского мы встретились с квадратами натуральных чисел, на предьщуших уроках мы уже повторяли их свойства.
Кстати, закономерность, о которой пойдет сейчас речь, впервые заметил А.Н.Колмогоров ещё в шестилетнем возрасте. По его учебникам и сейчас учатся наши теперешние старшеклассники.
Закономерность 1
Сделайте вывод: Сумма первых n нечетных чисел равна квадрату n
12 = 1
22 = 1+3
32 = 1 +3 + 5
…
72 = 1 + 3 + 5 + 7 + 9 + 11 + 13
Закономерность 2
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
400 |
441 |
484 |
529 |
576 |
625 |
Сумма трёх чисел, записанных в трёх клеточках "уголком" слева, равна четвёртому, записанному внизу справа.
Перед вами ещё несколько закономерностей:
Закономерность 3
Проверьте эту закономерность для n=5. Сделайте вывод: сумма кубов n натуральных чисел равна квадрату суммы этих n первых натуральных чисел.
13+23 ==(1+2)2
13+23 +33 ==(1+2+3)2
13+23 +33+43==(1+2+3+4)2
Закономерность 4
Рассмотрите следующие равенства. Запишите и проверьте правильность последующих равенств такого же типа
| 9 · 1 + 2 = 11 | 8· 1 + 1 = 9 | 9·9+7 = 88 |
| 9 · 12 + 3 = 111 | 8·12 + 2 = 98 | 9·98 + 6 = 888 |
| 9 · 123 + 4 = 1111 | 8·123 + 3 = 987 | 9·987+5 = 8888 |
| 9 · 1234 + 5 = 11111 | 8·1234 + 4 = 9876 |
Какие можно подметить здесь привила?
Итак, сегодня на уроке мы с вами увидели красоту цифр, чисел натуральных. В математике, ребята, есть своя красота, таких красивых последовательностей немного. Знайте их, умейте их видеть.
Я думаю, что вы будете интересоваться различными математическими диковинками, курьёзами.
Это вам будет любопытно, так же как и мне.
Еще С. В. Ковалевская говорила: «Математик должен быть поэтом в душе»
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Факультативное занятие "Задачи занимательной алгебры"

Разделы: Математика
I. «Яблоки»
Садовник продал первому покупателю половину всех своих яблок и ещё пол-яблока, второму покупателю – половину оставшихся и ещё пол-яблока, третьему – половину оставшихся и ещё пол-яблока и т.д. Седьмому покупателю он продал половину оставшихся яблок и ещё пол-яблока. После этого яблок у него не осталось. Сколько яблок было у садовника?
Решение:
Если первоначальное количество яблок х, то первый покупатель получил второй , третий , …, седьмой покупатель .
Получаем уравнение
или (х+1).
Вычисляя стоящую в скобках сумму членов геометрической прогрессии, получим
Всего было 127 яблок.
Ответ: 127 яблок.
II. «Трудная задача»
Картина Богдана Бельского «Трудная задача» известна многим, но мало кто из видевших эту картину вникал в содержание той «трудной задачи», которая на ней изображена. Состоит она в том, чтобы устным счетом быстро найти значение выражения
Задача, в самом деле, нелегкая. С нею, однако, хорошо справлялись ученики того учителя, который с сохранением портретного сходства изображен на картине, именно С.А.Рачинского, профессора естественных наук, покинувшего университетскую кафедру, чтобы сделаться рядовым учителем сельской школы. Талантливый педагог культивировал в своей школе устный счет, основанный на виртуозном использовании свойств чисел. Числа 10, 11, 12, 13 и 14 обладают любопытной особенностью: 102 +112 +122=132+142.
Так как 100 + 121 + 144 = 365, то легко рассчитать в уме, что воспроизведенное на картине выражение равно 2.
Алгебра дает нам средство поставить вопрос об этой интересной особенности чисел более широко: единственный ли это ряд из пяти последовательных чисел, сумма квадратов трех их которых равна сумме квадратов двух последних?
Решение:
Обозначив первое из искомых чисел через х, имеем уравнение
Удобнее, однако, обозначить через х не первое, а второе из искомых чисел. Тогда уравнение будет иметь более простой вид
Раскрыв скобки и сделав упрощения, получаем: х2 – 10х – 11 = 0,
откуда х = х1 = 11, х2 = .
Следовательно, существуют два ряда чисел, обладающих требуемым свойством: ряд Рачинского 10, 11, 12, 13, 14 и ряд
В самом деле, = .
III. «Задача Эйлера»
Стендаль в «Автобиографии» рассказывает следующее о годах своего учения: «Я нашел у него (учителя математики) Эйлера и его задачу о числе яиц, которые крестьянка несла на рынок…. Это было для меня открытием. Я понял, что значит пользоваться орудием, называемым алгеброй. Но, черт возьми, мне никто об этом не говорил…». Вот эта задача из «Введения в алгебру» Эйлера, произведшая на ум молодого Стендаля столь сильное впечатление.
Две крестьянки принесли на рынок вместе 100 яиц, одна больше, нежели другая; обе выручили одинаковые суммы. Первая сказала второй: «Будь у меня твои яйца, я выручила бы 15 крейцеров». Вторая ответила: «А будь у меня твои яйца, я выручила бы крейцера». Сколько яиц было у каждой?
Решение:
Пусть у первой крестьянки было х яиц, тогда у второй - (100 – х). Если бы первая имела (100 – х) яиц, она выручила бы 15 крейцеров. Значит, первая крестьянка продала яйца по цене за штуку. Таким же образом находим, что вторая крестьянка продавала яйца по цене за штуку.
Теперь определяется действительная выручка каждой крестьянки:
первой х = ,
второй (100-х) = .
Так как обе выручки одинаковы, то = .
После преобразования имеем: х2 + 160х – 8000 = 0, откуда х1 = 40, х2 = .
Отрицательный корень в данном случае не имеет смысла. У задачи только одно решение: первая крестьянка принесла 40 яиц, значит, вторая – 60.
Задача может быть решена еще другим способом, более кратким. Этот способ гораздо остроумнее, но зато отыскать его значительно труднее.
Предположим, что вторая крестьянка имела в k раз больше яиц, чем первая. Выручили они одинаковые суммы. Это значит, что первая крестьянка продавала свои яйца в k раз дороже, чем вторая. Если бы перед торговлей они поменялись яйцами, то первая крестьянка имела бы в k раз больше яиц, чем вторая и продавала бы их в k раз дороже. Это значит, что она выручила бы в k2 больше денег, чем вторая. Следовательно, имеем:
k2 = 15: 6 = отсюда k = .
Теперь остается 100 яиц разделить в отношении 3:2. Легко находим, что первая крестьянка имела 40, а вторая 60 яиц.
Ответ: 40 и 60 яиц.
IV. «Стая обезьян»
Другую индусскую задачу я имею возможность привести в стихотворной передаче, так как ее перевел автор превосходной книжечки «Кто изобрел алгебру?» В.И.Лебедев:
На две партии разбившись, Забавлялись обезьяны. Часть восьмая их в квадрате В роще весело резвилась; Криком радостным двенадцать Воздух свежий оглашали. Вместе сколько, ты мне скажешь, Обезьян там было в роще?
Решение:
Если общая численность стаи х, то откуда х1 = 48, х2 = 16.
Задача имеет два положительных решения: в стае могло быть или 48 обезьян, или 16. Оба ответа вполне удовлетворяют задаче.
Ответ: 16 или 48 обезьян.
V. «Вечеринка»
На вечеринке было 20 танцующих. Мария танцевала с семью танцорами, Ольга – с восьмью, Вера – с девятью и так далее до Нины, которая танцевала со всеми танцорами. Сколько танцоров (мужчин) было на вечеринке?
Решение:
Задача решается очень просто, если удачно выбрать неизвестное. Будем искать число не танцоров, а танцорок, которое обозначим через n:
1-я, Мария, танцевала с 6 + 1 танцорами
2-я, Ольга, танцевала с 6 + 2 танцорами
3-я, Вера, танцевала с 6 + 3 танцорами …
n-я, Нина, танцевала с 6 + n танцорами.
Имеем уравнение n + (6 +n) = 20, откуда n = 7, а, следовательно, число танцоров –
20 – 7 = 13.
Ответ: 13 танцоров.
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
«Трудная задача» — Математика, информатика, преподавание
В русскоязычных книгах по занимательной математике нередко встречается репродукция картины Богданова-Бельского «Трудная задача» (она же «Устный счёт»). Сколько себя помню, суть этой картины всегда вызывала у меня недоумение.
Если присмотреться, то на доске написано выражение\[\frac{10^2+11^2+12^2+13^2+14^2}{365},\]которое и предлагается посчитать в уме. В этом, собственно, «трудная задача» и состоит.

Когда я впервые это увидел — а это было лет в одиннадцать, — то просто посчитал «в лоб». Квадраты натуральных чисел я помнил где-то до \(20^2=400\), а сложить в уме несколько трёхзначных чисел не является таким уж интеллектуальным подвигом. Вычисление облегчилось ещё и тем, что у меня почти сразу получилось \(10^2+11^2+12^2=100+121+144=365\), это давало единицу в результат. Далее аналогично получилось \(13^2+14^2=169+196=365\), это дало ещё единицу, и ответ получился равным двум. Книжка подтверждала мой ответ, но почему-то добавляла, что вычисление основано на замечательном факте \(10^2+11^2+12^2=13^2+14^2\). Я же в этом факте абсолютно ничего замечательного не видел — ну то есть от слова «совсем».
Подумал: ну ладно, бывает. Кому-то показалось интересным, а мне нет. Дело вкуса, о вкусах не спорят. Но сколько раз я потом не встречал это выражение в книгах у самых разных авторов, и везде — «замечательный факт», «замечательный факт»…
Когда эти же слова с пафосным придыханием произнесла какая-то очередная учительница (это уже классе в восьмом было), я не выдержал и высказал своё недоумение вслух. Дескать, чего толку-то в этом факте? Было бы это свойство пяти последовательных целых чисел хоть сколько-нибудь распространённым или характерным — может и был бы толк. А так может существовать не более двух таких пятёрок, ну и что с того?! Что ж теперь — каждую подобную ерунду знать и помнить, что ли?!
С меня потребовали объяснить моё утверждение про «не более двух таких пятёрок». Я пожал плечами и озвучил очевидный, как мне казалось, факт: уравнение \[x^2+(x+1)^2+(x+2)^2 = (x+3)^2+(x+4)^2\tag{1}\] является по сути квадратным и может иметь не более двух различных решений.
Пока учительница переваривала моё утверждение, я раскрыл в этом уравнении скобки, упростил его и нашёл оба решения: \(x_1=10\), \(x_2=-2\). И радостно заявил, что второе из этих решений намного более интересно, нежели десятка.
Учительница поинтересовалась, почему я так считаю. Я пояснил, что оно удовлетворяет не только (1), но и симметричному с ним уравнению \[x^2+(x+1)^2 = (x+2)^2 + (x+3)^2+(x+4)^2\tag{2}.\] Подумал немного и сказал, что даже более того, если в (1) и (2) заменить вторые степени на любые чётные, то \(x=-2\) всё равно будет оставаться корнем, чего про десятку говорить нельзя.
Мне сообщили, что я не способен ценить красоту чисел и велели сесть. :) В общем, стороны остались при своих мнениях.
Впрочем, нет худа без добра: играясь со свойствами типа (1)-(2), я нашёл несколько любопытных уравнений: \[\begin{aligned}(x+1)^1 + (x+2)^2 + (x+3)^3 &= (x+4)^4\\(x-1)^1 — (x-2)^2 + (x-3)^3 &= 0\\(x-1)^1 — (x-2)^2 + (x-3)^3 — (x-4)^4 &= 0\end{aligned}\] У них у всех есть целочисленные решения и, пожалуй, по нынешним временам эти уравнения вполне потянут на олимпиадные задачи.
blog.balandin.guru
О квадратах двузначных чисел и не только о них…
Текущий год связан с двумя «маленькими» юбилеями.
180-летием выдающегося русского ученого и педагога Сергея Александровича Рачинского (1833-1902) и 145-летием замечательного русского художника, Академика живописи Николая Петровича Богданова-Бельского(1868-1945). Между этими двумя событиями есть прямая связь. Обнаружить ее можно на известной картине Н.П. Богданова-Бельского «Устный счет. В народной школе С.А. Рачинского», написанной в 1895-м году и находящейся в Государственной Третьяковской Галерее.
Учитель, давший деревенским ребятам «трудную задачу», это и есть С.А. Рачинский, изображенный художником с фотографической точностью.
* * *
Когда-то, в году примерно 1962-м, наша «математичка», Любовь Иосифовна Драбкина, дала эту задачу и нам, 7-классникам.
Я тогда очень увлекался только что появившимся КВН-ом. Болел за команду подмосковного города Фрязино. «Фрязинцы» отличались особым умением применять логический «экспресс-анализ» для решения любой задачи, «вытягивания» самого каверзного вопроса.
Быстро посчитать в уме я не мог. Однако, применив «фрязинский» метод, я прикинул, ответ должен выражаться целым числом. Иначе - это уже не «устный счет»! Этим числом не могла быть единица – даже если бы в числителе стояли одинаковые 5 сотен, ответ получался явно больше. С другой стороны, и до числа «3» он явно де дотягивал.
– Два!!! – выпалил я, на секунду опередив моего друга, Леню Струкова, лучшего математика нашей школы...
Текущий год связан с двумя «маленькими» юбилеями.
180-летием выдающегося русского ученого и педагога Сергея Александровича Рачинского (1833-1902) и 145-летием замечательного русского художника, Академика живописи Николая Петровича Богданова-Бельского(1868-1945). Между этими двумя событиями есть прямая связь. Обнаружить ее можно на известной картине Н.П. Богданова-Бельского «Устный счет. В народной школе С.А. Рачинского», написанной в 1895-м году и находящейся в Государственной Третьяковской Галерее.
Учитель, давший деревенским ребятам «трудную задачу», это и есть С.А. Рачинский, изображенный художником с фотографической точностью.
Представитель старинного дворянского рода, профессор, получивший в тридцать три года кафедру естественных наук в Московском университете, он, через два года, неожиданно оставляет службу («Чин следовал ему – он службу вдруг оставил. В деревне книжки стал читать»…). В отличие от персонажа А.С. Грибоедова, Сергей Александрович избрал другой, более активный и действенный способ «хождения в народ». Он не просто сам «читал книжки», а делал все возможное, чтобы их читали крестьянские дети – надежда и будущее России.
В своем родовом имении – селе Татево Бельского уезда Смоленской губернии, Сергей Александрович, на свои средства, строит сельскую школу. Всего же, в других селах Смоленской губернии, он построит свыше 20 подобных школ, 4 из которых будет содержать полностью. Свой богатейший педагогический опыт он обобщит в книге «Сельская школа», по выходе которой будет избран членом-корреспондентом Академии Наук по отделению русской словесности. Он станет всероссийски-известным человеком, получит личную благодарность от Государя Императора Николая II, но главной заботой педагога останутся его ученики. Многих из них он «выведет в люди», оказывая ребятам материальную поддержку, ходатайствуя об их принятии в те или иные учебные заведения.
Одним из таких учеников окажется способный юный рисовальщик Коля Богданов. «Внебрачный», «Богом данный» сын батрачки, прибавивший в будущем к своей фамилии название родного уезда.
Посмотрим на картину еще раз.
Обратим внимание на мальчика на переднем плане с выразительными, совсем не детскими глазами и сравним его с автопортретом Н.П. Богданова-Бельского (1915), находящимся в Луганском областном художественном музее (Украина).
Некоторые специалисты и многие любители живописи полагают, что в образе этого мальчика художник запечатлел самого себя…
* * *
Картины Н.П. Богданова-Бельского разбросаны по всему миру. Одна из них есть и в наших краях («Последняя воля». Таганрогский художественный музей).
История этого полотна необычна.
В 1925-м году оно было передано в Таганрогскую картинную галерею (так тогда именовался музей) из коллекции Румянцевского музея. В 1943-м году картина, вместе с другими полотнами, была похищена отступавшими немецкими войсками.
Уже в наши дни, «всплыв» на одном из европейских аукционов, она была приобретена частным лицом, пожелавшим остаться неизвестным. Однако, при содействии руководства Таганрогского металлургического завода (ТАГМЕТа), картина была у этого «лица» перекуплена. Наконец, 14 октября 2008-го года она вернулась в Таганрог. В торжественной церемонии принял участие тогдашний министр культуры России Александр Авдеев.
* * *
…Вернемся, однако, к «Устному счету». Уж очень он притягателен!
На доске написано условие задачи - определить значение дроби:
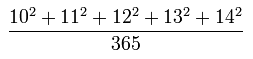
Когда-то, в году примерно 1962-м, наша «математичка», Любовь Иосифовна Драбкина, дала эту задачу и нам, 7-классникам.
Я тогда очень увлекался только что появившимся КВН-ом. Болел за команду подмосковного города Фрязино. «Фрязинцы» отличались особым умением применять логический «экспресс-анализ» для решения любой задачи, «вытягивания» самого каверзного вопроса.
Быстро посчитать в уме я не мог. Однако, применив «фрязинский» метод, я прикинул, ответ должен выражаться целым числом. Иначе - это уже не «устный счет»! Этим числом не могла быть единица – даже если бы в числителе стояли одинаковые 5 сотен, ответ получался явно больше. С другой стороны, и до числа «3» он явно де дотягивал.
– Два!!! – выпалил я, на секунду опередив моего друга, Леню Струкова, лучшего математика нашей школы.
– Да, действительно два, – подтвердил Леня.
– Как Вы считали? – спросила Любовь Иосифовна.
– Я никак не считал. Интуиция – ответил я под хохот всего класса.
– Если не считал – ответ не считается – «скаламбурила» Любовь Иосифовна. Леня, а ты тоже не считал?
– Нет, почему же, степенно ответил Леня. Надо было сложить 121, 144, 169 и 196. Я попарно сложил числа первое и третье, второе и четвертое. Так удобнее. Получилось 290+340. Общая сумма, включая первую сотню – 730. Делим на 365 – получаем 2.
– Молодец! Но на будущее запомните – в ряду двузначных чисел – у первых пяти его представителей – есть удивительное свойство. Сумма квадратов первых трех чисел ряда (10, 11 и 12) равна сумме квадратов следующих двух (13 и 14). И равняется эта сумма 365. Легко запомнить! Столько дней в году. Если год не високосный. Зная это свойство, ответ можно получить за секунду. Без всякой интуиции…
* * *
…Прошли годы. Наш город обзавелся своим «Чудом Света» – мозаичными картинами в подземных переходах. Переходов было много, картин – еще больше. Темы были самыми разными – оборона Ростова, космос… В центральном переходе, под перекрестком Энгельса (сейчас – Большая Садовая) – Ворошиловский сделали целую панораму об основных этапах жизненного пути советского человека – родильный дом – детский сад - школа, выпускной бал…
На одной из «школьных» картин можно было увидеть знакомую сцену – решение задачи… Назовем ее так: «Задачи Рачинского»…
…Проходили годы, проходили люди… Веселые и грустные, молодые и не очень. Кто-то вспоминал свою школу, кто-то при этом «шевелил мозгами»…
Замечательно поработали мастера-плиточники и художники, которыми руководил Юрий Никитович Лабинцев! К этой теме мы еще вернемся.
Сейчас «ростовское чудо» «временно недоступно». На первый план вышла торговля – в прямом и переносном смысле. Все же, будем надеяться, что в этом расхожем словосочетании – главным является слово «временно»…
Источники фото:http://julpalna.livejournal.com/275264.htmlhttp://www.bibliotekar.ru/kBogdanov/01.htmhttp://www.bibliotekar.ru/kBogdanov/
...
www.viskra.ru
Трудная задача - рассказ Николая Носова
Предлагаем ознакомиться с рассказом Николая Носова «Трудная задача».
 Рассказ «Трудная задача»
Рассказ «Трудная задача»Рассказ «Трудная задача» читать онлайн
Раз как-то зимой Федя Рыбкин пришел с катка. Дома никого не было. Младшая сестра Феди, Нина, уже успела сделать уроки и пошла играть с подругами. Мать тоже куда-то ушла.
— Вот и хорошо! — сказал Федя. — По крайней мере, никто не будет мешать делать уроки.
Он включил радио, достал из сумки задачник и стал искать задачу, которую задали на дом.
— Передаем концерт по заявкам, — объявил голос по радио.
— Концерт — это хорошо, — сказал Федя. — Веселей будет делать уроки.
Он подкрутил радио, чтоб было погромче, и сел за стол.
— Ну-ка, что тут нам на дом задано? Задача номер шестьсот тридцать девять. «На мельницу доставили четыреста пятьдесят мешков ржи, по восемьдесят килограммов в каждом…»
Из репродуктора послышались звуки рояля, и чей-то голос запел густым басом:
Жил-был король когда-то, При нем блоха жила. Милей родного брата Она ему была.— Вот какой противный король! — сказал Федя. — Блоха ему, видите ли, милей родного брата!
Он почесал кончик носа и принялся читать задачу сначала:
— «На мельницу доставили четыреста пятьдесят мешков ржи, по восемьдесят килограммов в каждом. Рожь смололи, причем из шести килограммов зерна вышло пять килограммов муки…»
Блоха! Ха-ха! -засмеялся певец и продолжал петь:
Позвал король портного: - Послушай, ты, чурбан! Для друга дорогого Сшей бархатный кафтан.— Ишь что еще выдумал! — воскликнул Федя. — Блохе — кафтан! Интересно, как портной его шить будет? Блоха ведь маленькая!
Он прослушал песню до конца, но так и не узнал, как портной справился со своей задачей. В песне ничего про это не говорилось.
— Плохая песня, — решил Федя и опять принялся читать задачу:
— «На мельницу доставили четыреста пятьдесят мешков ржи, по восемьдесят килограммов в каждом. Рожь смололи, причем из шести килограммов зерна…»
Ах вы сети, мои сени, Сени новые мои... -запел репродуктор снова.
— Интересно, что такое сени? — сказал Федя. — Гм!
Он потер обеими руками уши, словно они у него замерзли, и, стараясь не обращать внимания на радио, принялся читать задачу дальше:
— «Из шести килограммов зерна вышло пять килограммов муки. Сколько понадобилось машин для перевозки всей муки, если на каждой машине помещалось по три тонны муки?»
Пока Федя читал задачу, песенка про сени кончилась и началась другая.
Легко на сердце от песни веселой, Она скучать не дает никогда, И любят песню деревни и села, И любят песню большие города!Эта песенка очень понравилась Феде. Он даже забыл про задачу и стал пристукивать карандашом по столу в такт.
— Хорошая песня! — одобрил он, когда пение кончилось. — Так… О чем тут у нас говорится? «На мельницу доставили четыреста пятьдесят мешков ржи…»
Однозвучно гремит колокольчик, -послышался высокий мужской голос из репродуктора.
— Ну, гремит и пусть гремит, — сказал Федя. — Нам-то какое дело? Нам надо задачу решать. На чем тут мы остановились? Так… «Для дома отдыха купили двадцать одеял и сто тридцать пять простынь за двести пятьдесят шесть рублей. Сколько денег уплатили за купленные одеяла и простыни в отдельности…» Откуда тут еще одеяла с простынями взялись? У нас разве про одеяла? Да это не та задача! Где же та?.. А, вот она! «На мельницу доставили четыреста пятьдесят мешков ржи…»
По дороге зимней, скучной Тройка борзая бежит, Колокольчик однозвучный Утомительно гремит...— Опять про колокольчик! — воскликнул Федя. — На колокольчиках помешались! Так… Утомительно гремит… в каждом мешке… рожь смололи, причем из шести килограммов муки вышло пять килограммов зерна… То есть муки вышло, а не зерна! Совсем запутали!
Колокольчики мои, цветики степные! Что глядите на меня, темно-голубые?— Тьфу! — плюнул Федя. — Прямо деваться от колокольчиков некуда! Хоть из дому беги, с ума можно сойти!.. Из шести килограммов зерна вышло пять килограммов муки. Спрашивается, сколько понадобилось машин для перевозки всей муки…
Не счесть алмазов в каменных пещерах, Не счесть жемчужин в море полуденном.— Очень нам нужно еще алмазы считать! Тут мешки с мукой никак не сосчитаешь! Прямо наказание какое-то! Двадцать раз прочитал задачу — и ничего не понял! Задают же такие трудные! Ни за что не решить! Пойду-ка к Юре Сорокину. Он хорошо задачи решает — может, с ним вдвоём решим такую трудную задачку.
shkolnaiapora.ru
СЕКРЕТ «ТРУДНОЙ ЗАДАЧИ» | sibac.info
СЕКРЕТ «ТРУДНОЙ ЗАДАЧИ»
Мамедяров Даглар Мамедярович
канд. пед. наук, «Социально – педагогический институт», РФ, г. Дербент
THE SECRET OF “A CHALLENGING TASK”
Daglar Mamedyarov
candidate of Pedagogical Sciences, “Social Pedagogical Institute” , Russia, Derbent
АННОТАЦИЯ
В статье Секрет «Трудной задачи» автор рассматривает особенности чисел ряда Рачинского и аналогичных последовательностей.
ABSTRACT
In the article the secret of "a challenging task” the author examines the characteristics of Rachinskiy’s sequence of numbers and similar sequences.
Ключевые слова: Рачинский, последовательности.
Keywords: Rashinskiy; sequences.
В конце XIX века живописец-жанрист Н.Б. Богданов-Бельский (1868—1945) написал картину «Трудная задача». Мало кто из видевших эту картину вникал в содержание той «трудной задачи», которая на ней изображена. На ней изображена группа учеников сельской школы, задумавшихся над решением в «уме» задачи С.А. Рачинского, профессора естественных наук, покинувшего университетскую кафедру, чтобы сделаться рядовым учителем сельской школы. Талантливый педагог культивировал в своей школе устный счет, основанный на виртуозном использовании свойств чисел. На доске написано:
Действительно, нелегкая задача для быстрого решения в «уме», если не знать «секрета». А «секрет» очень прост. Дело в том, что и . Следовательно, искомый ответ 2.
Обратим внимание на другое. Из сопоставления выше написанных равенств следует, что , то есть сумма квадратов нескольких последовательных чисел, равна сумме квадратов следующих чисел. Число слагаемых в левой части равенства только на одно больше, чем в правой. (Заметим, что ).
Алгебра дает нам средство поставить вопрос об этой интересной особенности ряда чисел более широко:
1. Имеются ли, кроме чисел 3 и 4, другие два последовательные числа, сумма квадратов которых была равна квадрату следующего за ними числа, а кроме чисел 10, 11, 12, другие три последовательных числа, сумма квадратов которых была бы равна сумме квадратов двух непосредственно за ними следующих чисел?
2. Можно ли образовать равные суммы квадратов последовательных натуральных чисел, состоящие из четырех и трех слагаемых, из пяти и четырех слагаемых и вообще из и возрастающих слагаемых? [1. с. 198].
Ответ на эти вопросы можно найти в решении такой вполне доступной задачи:
Найти последовательных чисел, сумма квадратов которых равна сумме квадратов следующих чисел. Обозначив через первое из искомых чисел, имеем уравнение: . Раскрыв скобки и сделав упрощение, получаем или . Отсюда , .
Получаем два ряда чисел, обладающих требуемым свойствам: 3, 4, 5, и -1, 0, 1.
В самом деле и .
Теперь решим такое уравнение . Имеем: или
. Отсюда . Существует два ряда чисел, обладающих требуемым свойством; ряд Рачинского 10, 11, 12, 13, 14 и ряд -2, -1, 0, 1, 2. В самом деле .
Рассмотрим уравнение . Раскрыв скобки получаем:
или
. Имеем два ряда чисел; 21, 22, 23, 24, 25, 26, 27 и -3, -2, -1, 0, 1, 2, 3.
и . На два первых вопроса получили утвердительный ответ. Как уже заметили, эти последовательности являются арифметическими прогрессиями с разностью 1. Возникает вопрос: существуют ли другие последовательности с разностью 2, 3, 4. и т. д., обладающие требуемым свойством?
Решим уравнение .
, .
=,
Если . Имеем ряд 3, 4, 5: .
. Имеем ряд 6, 8, 10: .
. Имеем ряд 9, 12, 15: .
. Имеем ряд 12, 16, 20: и т. д.
Если , тогда имеем 1, 0, -1: .
, тогда имеем 2, 0, -2: .
, тогда имеем -4, 0, 4: и т. д.
Рассмотрим такое уравнение:
.
Имеем:
Или
=,
Если
Тогда имеем ряды 20, 22, 24, 26, 28 и -4, -2, 0,2,4.
=, =.
На этот вопрос мы тоже можем ответить утвердительно. Существует бесконечное множество последовательностей, отвечающих требуемому условию.
Теперь поставим такой вопрос. Существуют ли последовательности обладающие таким же свойством, где в левой части количество слагаемых больше чем в правой на 2, 3, 4 и т.д.?
Тогда наши уравнения в общем виде выглядят таким образом:
=
слагаемых
слагаемых, где .
Решая и анализируя много уравнений я установил, что коэффициенты квадратного уравнения , к которому приводится данное уравнение, имеют следующий вид: ;
. Это для последовательности, где . В общем виде:
), . По этим формулам мы легко можем составить квадратное уравнение для любых
Составим несколько уравнений для
Пусть .
. Получаем уравнение
. Если . Уравнение имеет вид .
Если . Уравнение принимает вид и т.д.
Пусть .
.Уравнение принимает вид
.
Пусть .
. Уравнение имеет вид
.
Пусть .
. Уравнение принимает вид
.
Дискриминанты этих квадратных уравнений при любых и являются точными квадратами. Составим несколько уравнений при .
Пусть
.
. Уравнение принимает вид
.
Пусть Тогда .
. Уравнение принимает вид
.
Составим уравнение при ,
тогда .
. Уравнение принимает вид .
, тогда .
. Уравнение принимает вид .
Заметим, что при любых уравнение имеет вид =0.
Уравнения получаемые при не имеют решения в целых числах. Вернее, мне не удалось найти уравнение, где дискриминант был бы точным квадратом.
Существуют ли последовательности, где число слагаемых в левой части больше числа слагаемых в правой на 2 и 3 и т. д., и обладающим вышеуказанным свойством? Этот вопрос остается открытым.
Теперь рассмотрим последовательности, получаемые при .
Эта пирамида обладает интересными свойствами.
1. Разность сумм слагаемых в левой и правой частях равна половине числа, равноудаленного от концов последовательности и т. д.
2. Число в середине последовательности равно удвоенному произведению числа слагаемых в левой и правой частях.
3. Сумма чисел в середине двух соседних последовательностей пирамиды является точным квадратом.
4. Дискриминанты уравнений, получаемых при являются точными квадратами и равны квадрату удвоенного треугольного числа , то есть квадрату половины числа в середине последовательности.
«Секрет» Трудной задачи поставил перед нами еще более трудную задачу: при каких натуральных , число
является точным квадратом?
Список литературы:
1.Перельман Я.Н. Занимательная алгебра. М.: АСТ; Астрель; Аст М., 2009 — с. 289.
sibac.info
Математический КВН. 8-й класс

Разделы: Математика
Уважаемые участники КВН! Наш КВН посвящен самой древней и самой юной, вечно молодой науке-математике.
Математика всегда сопровождает человека в жизни. Она помогает развитию других наук, она развивает у человека такие важные качества, как:
– логическое мышление, – хорошую память, – умение логически мыслить, – способность к творчеству, – работоспособность, – находчивость и смекалку, – интуицию и т.д.
Уместно напомнить такие цитаты :
“В любом открытии 99% труда и только 1% таланта и способностей”.
“Вдохновение – это такая гостья, которая не любит посещать ленивых”.
Систематическое занятие математикой обогащает человека, облагораживает его. Тот, кто хоть раз испытал радостное чувство от решения трудной задачи – тот будет стремиться познать еще и использовать полученные знания в жизни.
Во многих современных профессиях нужны математические знания : агроному и инженеру, рабочему и доярке, космонавту и дипломату, продавцу и кассиру. Даже домохозяйке для ведения домашнего хозяйства, для ремонта квартиры, для посещения магазина, почты и т.д. Неслучайно, великий математик Карл Гаусс сказал в XVIII в.:
“Математика – царица всех наук, а арифметика – царица математики”.
В игре КВН принимают участие две команды:
- Команда 8 класса.
- Команда 9 класса.
Слово для приветствия команде 8 класса.
Слово для приветствия команде 9 класса.
Первый конкурс “Разминка”.
Каждой команде предлагаются вопросы, на которые необходимо ответить через 1 минуту. За каждый верный ответ 2 балла.
Задание № 1.
Саша живет на 5 этаже, а Миша в два раза выше. На каком этаже живет Миша ?
Задание № 2.
По столбу высотой 10 метров взбирается улитка. За день она поднимается на 5 метров, а за ночь опускается на 4 метра. Сколько дней ей потребуется, чтобы достичь вершины столба ?
Задание № 3.
Дома на улице пронумерованы от 1 до 50. Сколько раз в нумерации встретится цифра 4 ?
Задание № 4.
Если в 12 часов ночи идет дождь, можно ли утверждать, что через 72 часа будет солнечная погода?
Задание № 5.
Груша дороже яблока в два раза. Что дороже : 8 яблок или 4 груши.
Задание № 6.
Если два петуха закричат изо всех сил, то человек проснется. Сколько петухов должны закричать, чтобы проснулось 4 человека ?
Второй конкурс. 2 минуты. 5 баллов.
Напротив названия каждого животного стоит какое-либо число. Какое число стоит напротив слова “ ослик” ?
Свинья – 3
Корова – 2
Собака – 3
Петух – 8
Утка – 3
Кошка – 3
Ослик – ?
Третий конкурс. 2 минуты. 5 баллов.
Командам предлагается математический софизм. Необходимо найти ошибку.
5 = 6
35 + 10 – 45 = 42 +12 -54
5 (7 + 2 – 9) = 6 (7 + 2 -9)
Сократим на 7 + 2 – 9
Получим:
5 = 6
Четвертый конкурс. 2 минуты. 5 баллов.
Между цифрами 8 расставить знаки +, чтобы получилось верное равенство.
8 8 8 8 8 8 8 8 = 1000
Пятый конкурс. 2 минуты. 5 баллов.
В пустые квадраты расставить числа 2, 3, 4, 5, 6, 8 так, чтобы произведение чисел в каждом столбике и в каждой строке равнялось 120.
Шестой конкурс. 2 минуты. 5 баллов.
Необходимо передвинуть одну цифру, чтобы получилось верное равенство.
101 – 102 = 1
Седьмой конкурс. “Темная лошадка”.
Угадать фамилию ученого. После каждой строчки количество баллов уменьшается на 1. Максимальное количество баллов: 7.
Темная лошадка.
Он – древнегреческий философ, религиозный и политический деятель…
Родился приблизительно в 580 году до нашей эры на острове Самос у берегов Эгейского моря…
У своего первого учителя он получил знания основ музыки и живописи…
Он учился астрологии, предсказанию затмений, тайнам чисел, медицине…
Он попал в персидский плен. В плену в Вавилоне он встретился с персидскими магами, приобщился к восточной астрологии и мистике…
Через 12 лет его освободил персидский царь Дарий. На Кротоне он создал свою собственную философскую школу…
Фамилию этого ученого знает каждый ученик школы из-за его знаменитой теоремы…
Восьмой конкурс. 5 баллов. “Слово три”.
Расскажу я вам рассказ В полтора десятка фраз Лишь скажу я слово “три” Приз немедленно бери
Однажды щуку мы поймали Распотрошили, а внутри Рыбешек мелких увидали, И не одну, а сразу …две.
Мечтает мальчик закаленный Стать олимпийским чемпионом Смотри, на старте не хитри, А жди команду : раз, два, ….марш.
Когда стихи запомнить хочешь, Их не зубри до поздней ночи, А про себя, их повтори Разок, другой, но лучше…пять
Недавно поезд на вокзале Мне три часа пришлось прождать Ну, что ж,друзья, вы приз не взяли
Девятый конкурс. 2 минуты. 5 баллов.
Когда внук спросил у деда сколько ему лет, внук ответил : “Если я проживу еще половину того, что я прожил и еще один год, то мне будет сто. Сколько лет деду? (66)
Десятый конкурс. 2 минуты. “Трудная задача” 5 баллов.
Вычислить. Картина “Трудная задача”.
(102+112+122+132+142):365
Подведение итогов.
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai










