Вечность бытия и непобедимость бесконечности жизни! Бесконечность картина
Передача бесконечности в картине
В этом параграфе нам бы хотелось упомянуть еще об одном изменении в представлении о пространстве, вызываемом центральной перспективой. В детских рисунках, во фресках древних египтян или росписях древнегреческих сосудов пространство сводится к зависимости между расстоянием, направлением и размерами изображаемых предметов. Освальд Шпенглер отмечал, что у греков не было слова для обозначения понятия «пространство». Они говорили только о расстоянии, месторасположении, протяженности и объеме. В средневековой живописи появляется расположение объектов, чаще всего запертое со всех сторон горами или стенами. Такое расположение хотя и являлось трехмерным, но тем не менее не означало ничего, кроме пространственных отношений, присущих только самой изображаемой сцене. Изометрическая перспектива радикально отличается от этих приемов пониманием пространства как самостоятельной сущности, выраженной в системе наклонно расположенных параллелей —системе, которой должны подчиняться все объекты. Этот способ передачи пространства не ограничивается лишь рамками картины. Параллели уходят далеко за ее пределы, и очень часто кажется, что объекты продолжаются за границами рамки, которая проходит как бы сквозь них. Таким образом, изометрическая перспектива указывает на бесконечность пространства. Однако все это остается, по существу, вне интересов человека, потому что изометрическая перспектива относится к пространству, являющемуся внешним по отношению к картине. Таким образом, вопрос остается, как это было и раньше, открытым.
В ландшафтах, изображаемых в произведениях китайских художников, бесконечность пространства выступает внутри картины как конечная цель зрительной линии, которая для глаза остается недосягаемой. Парадоксально, но в центральной перспективе бесконечность предполагает точное месторасположение в пространстве, имеющем конечный предел. Исчезающая точка как вершина пространственной пирамиды находится на определенном расстоянии, однако она олицетворяет собой бесконечность. Она находится в границах досягаемости инедосягаемости в одно и то же время, точно так же как предел в математических расчетах. Все объекты изображаются на картине таким образом, что в своем внешнее облике содержат зрительно воспринимаемую ориентацию относительно бесконечности, а бесконечность выступает самим центром ощутимого пространства. Наличие бесконечности в любом определении конечного есть, по мнению Шпенглера, характерная черта мышления современного европейца.
Интуитивно большинство художников маскировали неопределенное значение исчезающей точки ив своих произведениях не позволяливстречаться сходящимся линиям. С этой целью либовид горизонта закрывался каким-нибудь объектом, либо основное пространство оставалось пустым, либо исчезающая точка располагалась где-то за пределами границ картины. На ее специфическое месторасположение указывала вся перспективная конструкция, но тем не менее она оставалась недосягаемой. Мудрость этой методики можно осознать лишь тогда, когда случайно воспринимается: композиция, в которой действительно столкновение удаляющихся линий раскрывает нашему взору этот парадокс.
Наконец следует отметить, что центральная перспектива располагает бесконечность в определенном направлении. Все ото заставляет пространство казаться направленной струей, которая проникает в картину через ближние стороны и сходится где-тонарасстоянии при своем выходе из картины. В результате происходит превращение пространственной одновременности во временное явление, то есть в необратимую последовательность событий. Традиционное представление о существующем приобретает новое понимание событийного процесса. Таким путем центральная перспектива ознаменовала и положила началосущественному развитию понимания природы в западном искусстве.
1. J. J. Gibson, The perception of the visual world, Boston, 1950, p. 142.
- Имя главного действующего персонажа в сказке Л. Кэрролла «Алиса в стране чудес». — Прим. ред.
- W. Kohler and D. A. Emery, Figural aftereffects in the third dimension of visual space. «American Journal of Psychology», 1947, vol. 60, p. 176.
- К. Koffka, Some problems of space perception, в: Murchison, С. (ed.), Psychologies of 1930, Worcester, 1930, p. 166.
- Джорджо Вазари, Жизнеописании наиболее знаменитых живописцев, ваятелей и зодчих. «Искусство», М., 1956, т. I, стр. 70.
- М. М о г 1 е a u-Ponty, Phenomenologie de la perception, Paris. 1945, p. 294—309.
- С. В. Hochberg and J. Е. Н о с h b е г g, Familiar size and the perception of depth, «Journal of Psychology», 1952, vol. 34, p. 107—114.
- J.Gibson, The perception of the visual world, Boston, 1950.
Глава шестая
СВЕТ
Если мы имеем дело с частым повторением какого-либо события илис неоднократным восприятием какой-нибудь вещи и научились реагировать на них совершенно спокойно, то, по всей вероятности, наш разум и наши чувства не будут активно на них откликаться. И все же это наиболее элементарные и общие реакции, которые с яркой непосредственностью раскрывают природу всего существующего.
Восприятие света
Свет представляет собой один из существенных элементов жизни. Для человека, как и для всякого животного, ведущего дневной образ жизни, свет является условием для наиболее активной деятельности. Он есть визуальное дополнение другой одухотворяющей силы — теплоты. Свет раскрывает нашему восприятию сущность смены суток и времен года, которая заключается в восстановлении жизненных сил. Свет — это один из наиболее впечатляющих источников наших ощущений. Не случайно на ранних стадиях развития религиозных обрядов его почитали и молились ему. Но как только его сила была в достаточной степени познана в повседневной практической деятельности людей, появилась угроза предать его свойства забвению. Для художника и для обыкновенного, рядового человека в случае, когда у него появляется поэтическое вдохновение, свет сохраняет подступы в царство творчества, которое может приобретаться также благодаря созерцанию света.
Понятие художника о свете формируется под воздействием общей позиции человека и его реакции. Это осуществляется двумя путями. Во-первых, свет для художника представляет практический интерес как средство акцентировки внимания. Благодаря свету мы осознаем, что в нашем восприятии является обычным и поэтому не требующим от нас каких-то действий. Яркая вспышка молнии или неожиданное наступление темноты, вызванное затмением солнца, легко воспринимаются, а само восприятие вызывает определенные эмоции. А купание лучей солнца в листве зеленых кленов или же нежная гамма теней, которые, чередуясь с ярко освещенными местами, подчеркивают округлые формы яблока, обязательно привлекают наше внимание, так как возникает потребность отыскать какие-то связи в этой непоследовательности.
Во-вторых, представление художника о свете основывается на показаниях его собственных глаз — показаниях, которые уже сами по себе в значительной мере отличаются от взгляда ученого на физическую реальность. Даже общеизвестные факты трудно вытесняют данные непосредственного наблюдения. Прошло уже более четырехсот лет после появления учения Коперника, а солнце все еще продолжает двигаться по небу. Древняя геоцентрическая теория постоянного вращения солнца вокруг земли фактически никогда не подтверждалась зрительным восприятием. До сих пор солнце рождается на востоке, а умирает на западе. Сегодня наш глаз, вероятно, принял ту точку зрения, что мир не кончается там, где небесный свод касается горизонта, и, может быть, со временем мы привыкнем, что будем видеть землю и себя на земле вращающимися вокруг неподвижного солнца.
Физики убеждают нас в том, что свет, который нас окружает, заимствован. Свет, освещающий небо, послан через темную вселенную на темную землю солнцем с расстояния в сто пятьдесят миллионов километров. Это очень плохо согласуется с данными eго восприятия. Для глаза кажется, что небо освещено само по себе, а солнце есть не что иное, как его самая яркая характерная черта, возможно, порожденная небом. Согласно библейской «Книге Бытия», появление света породило первый день, в то время как солнце, луна и звезды были добавлены лишь на третий день. В беседах, которые проводил Пиаже с детьми, один семилетний ребенок заявил, что именно небо порождает свет. «Солнце не похоже на свет. Свет светит повсюду, а солнце — только там, где оно есть». А другой ребенок объясняет: «Всякий раз, когда солнце встает утром и видит, что погода сегодня плохая, оно уходит туда, где погода хорошая».
Таким образом, свет представляется самостоятельным явлением или же качеством, внутренне присущим самим предметам, а не воздействием, передаваемым от одного предмета к другому, «День» — это яркая вещь, о которой часто думают как о скоплении белых облаков, которые приходят извне и движутся по небесному своду. Таким же образом яркость предметов на земле воспринимается в основном как свойство их самих, а не как результат отражения. Не принимая во внимание особые условия, о которых будет сказано ниже, освещенность дома, дерева или лежащей на столе книги не воспринимается нами как какой-то подарок далекого источника. В лучшем случае дневной свет или свет электрической лампы освещают вещи подобно тому, как спичка поджигает охапку дров. Эти вещи менее ярки, чем солнце или небо, но в принципе не отличаются от них. Они просто менее яркие светила.
Соответствующим образом темнота воспринимается либо как угасание яркости, присущей предмету, либо как тот эффект, который получается, когда пытаются спрятать светлые предметы в тени темных. Ночь — это не отрицательный результат удаления света, но положительное появление темного покрывала, которое заменяет или покрывает день. Ночь, как она представляется детям, состоит из черных облаков, которые движутся так близко друг к другу, что белое никак не может пробиться сквозь них. Некоторые художники, такие, как Рембрандт или Гойя, по крайней мере в некоторых своих картинах, изображали мир как темное пространство, местами подсвечиваемое светом. Оказалось, что они подтвердили средствами искусства открытия, сделанные физиками. Однако, по-видимому, до сих пор господствует точка зрения, согласно которой свет, хотя и рождается из исконной темноты, является все же неотъемлемой принадлежностью неба, земли и предметов, обитающих на ней, а их яркость и освещенность периодически то появляются, то исчезают в зависимости от темноты.
Утверждать, будто бы все это — неправильные толкования, присущие только детям и первобытным людям, и что все это отвергнуто современной наукой, означало бы игнорировать весь визуальный опыт, который находит отражение в представлениях художников. Знание заставило нас отказаться от высказываний, подобно высказываниям детей, древних летописей или жителей Полинезии. Однако наше видение мира остается почти неизменным, потому что оно определяется непреодолимыми условиями восприятия, которые действуют везде и всегда. Тем не менее нас приучили полагаться больше на знания, чем на данные зрительного восприятия, до такой степени, что требуются усилия детей или художников, чтобы заставить пас ясно представить себе то, что мы видим.
Похожие статьи:
poznayka.org
Живопись ~ Бесконечность

«Талисман»
Акварель, 20х30 см, классический портрет
на заказ

«Зимний портрет»
Акварель, 20х30, классический портрет.
на заказ

«Гранаты» По мотивам Е.Базановой
Акварель, 20х30 см, натюрморт. Картина оформлена в паспарту и раму 35х45 см.
на заказ

«Петух»
Акварель, 25х35 см, анималистика Картина оформлена в раму
наличие

Портрет Шакиры
Акварель, 20х30 см
на заказ

«Мальчик в шапке»
Акварель, 30х40, классический портрет. Картина оформлена в паспарту и раму 40х50 см.
на заказ

«Мяу»
Акварель, 20х30 см, анималистика. Картина оформлена в паспарту и раму 30х40 см.
на заказ

«Слоны»
Акварель,20х30, анималистика Картина оформлена в паспарту и раму 30х40 см.
наличие

«Лимоны» (по мотивам Е.Базановой)
Акварель, пастель, 20х30 см, натюрморт. Картина оформлена в раму.
наличие

«Гармония»
Акварель,30х40 см, портрет. Картина оформлена в паспарту и раму 40х50 см.
наличие

«Une elegance»
Акварель, 25х35 см, портрет. Картина оформлена в паспарту и раму.
наличие

Уличное кафе
наличие

«Une magie»
Акварель, 30х40 см, портрет. Картина оформлена в раму.
наличие

«Алина»
Акварель, 20х30, портрет. Картина оформлена в раму.
наличие

«Severus Snape»
Акварель, 30х40 см, портрет. Картина оформлена в паспарту и раму 40х50 см.
на заказ

«Зима»
Акварель, 20х30 см, классический портрет
наличие

«Сова»
Акварель, 30х40 см, анималистика
наличие

«Бархат»
Акварель, 25х35 см, портрет. Картина оформлена в паспарту и раму.
наличие

«Сон»
Акварель, 30х40см, Картина оформлена в раму.
наличие

Субботнее утро
25х35 см акварель
на заказ

Василиса
Акварель, 20х30 см, классический портрет Watercolor 20x30 cm, portrait
наличие

«Портрет девочки»
Акварель, 20х30, классический портрет. Картина оформлена в паспарту и раму 30х40 см.
на заказ

Белая яхта
32х40 см, акварель
наличие

Портрет дирижера и пианиста В. Ашкенази
Акварель, 22х32 см
наличие

Роза. Вольная копия с этюда LaFe
Акварель, 30х20
наличие

Дирижер
25х35 см акварель
на заказ

Аромат сирени
30х40 см, акварель
наличие

Безысходность
23х35 см акварель
наличие

Щенок в корзине
Акварель, 20х30, анималистика
наличие

«Цветущая ветвь»
Акварель, 20х30 см Картина оформлена в паспарту и раму 30х40 см.
наличие

«Кот и бабочки»
Акварель, 20х30 см Анималистика
на заказ

Акварель, тушь, 20х30 см Картина оформлена в раму и паспарту
наличие

«Русь»
Акварель, 20х30 см, пейзаж
наличие

«Красные апельсины»
Акварель, 30х40 см, натюрморт
наличие

«Николас Альберто»
Акварель, 20х30 см
наличие

«Французский бульдог»
Акварель, 20х30 см
на заказ

Примирение
Акварель, 20х30, классический портрет.
наличие

«Зимняя прогулка»
Акварель, 20х30 см, классический портрет
наличие

«Туфли Марии Антуанетты»
Акварель, 20х30 см
на заказ

«Дольки арбуза»
Акварель, 20х30 см
наличие

В белом
Акварель, 20х30
наличие

Яхты Барселоны
22х35 см, акварель
наличие

Французский завтрак
Акварель, 25х20 см
на заказ

Aurora
Evgeniya Marki Watercolor, 2013 [email protected]
наличие

Hunting
Evgeniya Marki Watercolor, 2013 [email protected]
на заказ

Тайна
Evgeniya Marki Secret 35х27, 2014 [email protected]
наличие

воздушная балерина
20х30, пастель
наличие

Руки пианиста
Акварель, 25х25 см
наличие

Прогулка
Evgeniya Marki Watercolor 60х80, 2013 [email protected]
наличие

Мария-Антуанетта
Evgeniya Marki Watercolor 30х40, 2013 [email protected]
наличие

Балет
Акварель, 25х35
наличие

Прогулка с собачкой
Акварель, 30х40, работа оформлена в раму и паспарту
наличие

Март
Акварель, 20х30 см, классический портрет
наличие

«Легкость»
Акварель, 20х30 см, классический портрет
наличие

Дождливая Венеция
Evgeniya Marki "Raining Venice" watercolor, 40х30, 2014 [email protected]
наличие

В ресторане
Evgeniya Marki "In restaurante" Watercolor 30х20, 2013 [email protected]
наличие

Любопытные котята
Evgeniya Marki Watercolor 35х27, 2014 [email protected]
на заказ

Балерина
Пастель, 25х35 см, портрет. Картина оформлена в паспарту и раму.
на заказ

Бархат
Пастель, 25х35 см, анималистика Картина оформлена в паспарту и раму.
на заказ

Лебединое озеро
22х30 см, акварель
наличие

Марсель
22х35 см, акварель
наличие

Chefchaouen
Watercolor 20x30
наличие

Букет сирени
20х30 см, акварель
на заказ

Солнечный день
Акварель, 30х15 см
наличие

Маленькая балерина
Акварель, 20х30 см
наличие

Портрет малыша
20х30 см, акварель
на заказ

Sunny day
Watercolor, 20x20 cm portrait of Sasha Burimova
на заказ

На пляже
20х30 см, акварель
наличие

Русские борзые
30х40, акварель,работа оформлена в раму и паспарту
наличие

Завтрак
30х40 см, акварель, работа оформлена в раму и паспарту
наличие

Бульдог
Акварель, 30х40, работа оформлена в раму и паспарту
на заказ

После ошибки
Акварель, 30х40, работа оформлена в раму и паспарту
на заказ

Москва
30х40 см, акварель, работа оформлена в раму и паспарту
наличие

Слеза
Акварель, 30х40 см, классический портрет
наличие

Муза
Работа из серии "Утро на Сан-Оноре" Акварель, 40х50 см, оформлена в раму
наличие

Улицы Марокко
Акварель, 25х18
на заказ

Игра на фортепьяно
Акварель, 25х18, оформлена в раму и паспарту
на заказ

Красота востока
Акварель, 25х18
на заказ

Завтрак в Париже
Акварель, 22х35
на заказ

Разговор по телефону
Акварель, 25х18 см
на заказ

Утро на Сан-Оноре. Пробуждение
Работа из серии "Утро на Сан-Оноре" Акварель, пастель, 35х40 см
на заказ

Солнечное утро на Сан-Оноре
Работа из серии "Утро на Сан-Оноре" 35х45 см, акварель
наличие

Утро на Сан-Оноре
Работа из серии "Утро на Сан-Оноре" Акварель, 50х70 см
наличие

Саграда Фамилия
Акварель, 20х30 см
на заказ

Мелодия Арфы
Акварель, 30х25
наличие

Балетные этюды
Акварель, 30х20 см
наличие

Балетные этюды. Выступление
Акварель, 20х30 см
на заказ

Друзья
Акварель, 20х30
наличие

Портрет девушки в красном платье
Акварель, 30х40 см, оформлена в раму и паспарту
наличие
Счастливое утро
Акварель, 20х30, оформлена в раму и паспрту
наличие

Легкое дуновение ветра
Акварель, 20х30
наличие

Парижский завтрак
Акварель, 30х40 см, картина оформлена в раму и паспарту
наличие

кобальт
Акварель, 30х40
наличие

Мечтательница
Акварель, 30х40, работа оформлена в раму и паспарту
наличие
beskonechnost.com
Статья "Бесконечность и иллюстрация этого понятия в произведениях искусства"

Разделы: Математика, Внеклассная работа
“В мире нет места для некрасивой математики”, – писал Харди. Безусловно, не каждый человек может быть чувствительным к эстетической привлекательности математики, но есть люди, которым красота математики представляется как безусловная и несомненная реальность и кто в общении с этой красотой находит смысл и цель существования. Как возникает степень увлечённости математикой? Кому открывается её красота? Что такое “математический ум”? Это дар природы или результат воспитания? Можно задавать вопросы и задавать… Но на эти вопросы надо стремится дать ответы.
Безусловно, большинство студентов с обычными математическими способностями не отдают предпочтение математике, не ощущают в себе призвания к математике, не видят её красоту. Причины этого различные; но мы не будем останавливаться на этих причинах, а лучше постараемся более активно заниматься развитием творческих умов, желанию больше знать.
“Хочу знать – и весь сказ. Просто так! Потому что это – моя жизненная потребность, потому что без этого мне жизнь – не в жизнь. Хочу знать потому, что не могу не хотеть этого”, – так объяснял
А. Д. Александров своим студентам, когда они задали вопрос: “Зачем это Вам или нам нужно? Какую мы будем иметь от этого пользу?” А великий Данте в своей бессмертной поэме писал так:
Тот жалкий срок, пока ещё не спят Земные чувства, их остаток скудный Отдайте постиженью новизны, Чтоб солнцу вслед увидеть мир безлюдный, Подумайте о том, чьи вы сыны! Вы созданы не для животной доли, А к доблести и к знанью рождены! Поговорим о бесконечности.
Хорошей иллюстрацией этого понятия являются своеобразные графические работы профессора МГУ Анатолия Тимофеевича Фоменко, в том числе и эта, под которой надпись гласит: “Одна из реализацией идей математической бесконечности: “Загадочный мир”.
Кто же такой Анатолий Тимофеевич Фоменко? В числе авторов одного из первых учебников по топологии был студент пятого курса механико-математического факультета МГУ Анатолий Фоменко. Спустя два года он защитил кандидатскую диссертацию, а спустя еще два года – докторскую. “Анатолий Тимофеевич 1945 года рождения, академик Российской Академии наук (РАН), действительный член МАНВШ (Международной Академии наук Высшей Школы), доктор физико-математических наук, профессор, заведующий кафедрой механико-математического факультета Московского Государственного университета.
Анатолий Тимофеевич решил известную проблему Плато в теории спектральных минимальных поверхностей, над которой бились математики, создал теорию инвариантов интегрируемых гамильтоновых динамических систем. Лауреат Государственной Премии Российской Федерации 1996 года. Автор 180 научных работ, 26 математических монографий и учебников, специалист в области геометрии и топологии, вариационного исчисления, теории минимальных поверхностей, компьютерной геометрии. Автор нескольких книг по разработке и применению новых эмпирико-статистических методов к анализу исторических летописей, хронологии древности и средневековья.” “Нельзя
быть настоящим математиком, не будучи немного поэтом”, – писал известный немецкий математик Карл Вейерштрасс. Анатолий Фоменко не только математик, но к тому же его знают как... художника, историка, знатока музыки.
“Я очень люблю музыку, потому что она сродни математике, говорил Анатолий Фоменко. – И та и другая предполагают некий идеальный мир, который подвластен только его создателю. Язык этого мира условен: в – музыке - ноты, в – математике – формулы. Есть много общего и между образами музыкальными и математическими. И те и другие возникают где-то на стыке мысли, чувства, интуиции. Может, поэтому, чем лучше понимаешь музыку, тем увереннее чувствуешь себя в кругу математических понятий”, – писал Анатолий Фоменко.
Однажды я попала на выставку работ Фоменко. Меня поразили его картины. Через один из журналов мы с коллегами обратились к Анатолию Тимофеевичу с просьбой демонстрации репродукций его картин в нашем техникуме. Он любезно откликнулся на нашу просьбу и при личной встрече передал репродукции своих картин формата А2 преподавателю Шипову А.Е. во временное пользование. Наши студенты, после проведенных бесед и осмотра произведений искусства (данными репродукциями были увешаны стены двух аудиторий) вдохновились и пробовали рисовать картины с математическим содержанием. Мы благодарны Анатолию Тимофеевичу за этот бескорыстный поступок, который дал возможность понять сложные математические идеи посредством художественных графических образов, представленных на картинах.
В журнале “ “Техника молодежи” за 1985г. он пишет статью “Бесконечность в математике...”: “Логический аспект понятия “бесконечность” – безусловно, важный, но далеко не единственный. Возможно, настало время, опираясь на опыт современной математики и ее приложений, прейти от небольшого эскиза о бесконечности к созданию развернутого полотна, в котором отразились бы основные представления и мысли, что волнует физиков и математиков на протяжении многих десятилетий и даже столетий в связи с этим глубоким натурфилософским и математическим понятием.
Каждая область современной математики (геометрия, алгебра и т. д.) обладает своим “рисунком бесконечности”, связывает с этой идеей свой набор психологических образов и эмоций. Естественно, что нагляднее всего эти образы в геометрии. Геометрическая бесконечность наиболее доступна демонстрации и в то же время чрезвычайно сложна, поскольку часто вступает в конфликт с нашей геометрической интуицией. Дело в том, что физиологические механизмы восприятия, вероятно, не в состоянии адекватно реагировать на абстрактное интеллектуальное задание “представить геометрическую бесконечность”, и наш мозг вынужден подменять “подлинную бесконечность” интуитивно более понятным и грубым геометрическим объектом, иногда совершая при этом незаметную ошибку, подстановку.
Современная геометрия знает много примеров, в которых так или иначе присутствует бесконечная процедура (актуальная бесконечность), разрушающая в итоге наши привычные представления, сложившиеся на основе повседневного, “конечного” опыта. Этим обстоятельством удачно воспользовался при создании своих замечательных графических работ известный французский художник М.К. Эшер, гравюры которого неоднократно публиковались в нашей научно-популярной прессе”. В 2003г. У нас в Эрмитаже была выставка работ этого интересного художника. “ С одной стороны, он изображал “бесконечно сложные объекты”, а с другой – “невозможные объекты” (вечные двигатели и проч.), умело, эксплуатируя несовершенство и ограниченность нашей геометрической интуиции. При этом он опирался на математические конструкции, применяемые в современной алгебре, геометрии, кристаллографии и т. п. Именно глубоким проникновением в природу геометрической бесконечности и объясняется сильное воздействие на зрителя”, – писал Анатолий Фоменко.
Вариациями на тему “Бесконечность” мы можем считать и статью журналиста Вячеслава Жвирблиса из журнала “Техника молодежи”, который называется “Рассказ о бесконечности, сочиненный ночью на берегу теплого моря”. Приведу некоторые отрывки из этой статьи: “Бездонный ночной небосвод и неумолчный шум прибоя обычно помимо воли заставляют задуматься о бесконечности. Бесконечности пространства и бесконечности времени.
Бесконечность, впрочем, не столько привлекает, сколько пугает. Право, мороз пробегает по коже, когда испытываешь ее представление наглядно. Хотя математики такие же люди, как и все, они давно храбро бродят по необозримым просторам бесконечности. Как им это удается? Что нужно, скажем, для того, чтобы абсолютно точно записать число е, обозначающее основание натуральных логарифмов?
На этот вопрос может быть два ответа.
Ответ первый: Бесконечно большой лист бумаги и бесконечно большое время, ибо сколь мелко и быстро мы бы не писали цифры, заполнять ими бесконечно большую поверхность бесконечным рядом числа е = 2,71828... придется бесконечно долго. В этом случае говорят о потенциальной бесконечности, то есть бесконечности, которая существует только потенциально, так сказать, в принципе, но реально никогда не может завершиться.
Ответ второй: любой клочок бумаги и несколько
секунд, за которые можно набросать формулу,
позволяющую вычислить число е, с любой
наперед заданной точностью. Для этого в формулу  — нужно
лишь по очереди подставлять возрастающие до
бесконечности числа натурального ряда. Такую
операцию принято обозначать сочетанием символов
п –>
— нужно
лишь по очереди подставлять возрастающие до
бесконечности числа натурального ряда. Такую
операцию принято обозначать сочетанием символов
п –>  ; в этом случае бесконечность
называют актуальной как бы раз и навсегда
реально завершенной, реально существующей, хотя
и не равной ничему определенному.
; в этом случае бесконечность
называют актуальной как бы раз и навсегда
реально завершенной, реально существующей, хотя
и не равной ничему определенному.
Хитрость последнего приема заключается в том, что вся бесконечность упрятывается в короткое сочетание символов, в котором время участвует в замаскированном виде: ведь п надо все время увеличивать!
Само слово “бесконечность” говорит, казалось бы, о том, что это нечто, не имеющее ни начала, ни конца. Бесконечная линия, бесконечная плоскость, бесконечное пространство... Это – наглядный образ потенциальной бесконечности. А может ли считаться бесконечным конечный отрезок? Скажем, длиной в один сантиметр?
С точки зрения чистой математики, актуально бесконечно большим может считаться и отрезок длиной в один сантиметр, и отрезок, равный диаметру атома водорода или электрона. И вообще любой, сколь угодно малый, но конечный отрезок – все дело лишь в том, чем его измерять. Ведь если единица измерения бесконечно мала (вернее, стремится к нулю), то бесконечно велик (точнее, стремится к бесконечности) и размер любого измеренного с ее помощью отрезка.
Другими словами, бесконечно большая величина вовсе не обязана быть невообразимо большой. Она может иметь любые конечные (и даже крайне малые с нашей точки зрения) размеры, если для ее измерения используется величина бесконечно малая, то есть непрерывно уменьшающаяся во времени; но та же конечная величина может считаться и бесконечно малой, если она измеряется с помощью бесконечно возрастающей во времени величины.
То есть, по сути, у реальной физической бесконечности должны быть две неразрывно связанные друг с другом области – область бесконечно больших и область бесконечно малых, – и поэтому ее невозможно подразделять на потенциальную и актуальную. Такая бесконечность должна просто существовать”.
Вариацией на эту тему являются и стихи английского поэта Уильямса Блэйка:
“В одном мгновенье видеть Вечность, Огромный мир – в зерне песка В едином миге – бесконечность И небо – в чашечке цветка”.
И стихотворение Валерия Брюсова “Мир электрона”.
“Быть может, эти электроны - Миры, где пять материков, Искусства, званья, войны, троны И память сорока веков! Еще, быть может, каждый атом - Вселенная, где сто планет: Там, все, что здесь, В объеме сжатом Но также то, чего здесь нет. Их бесконечность, как и здесь, Там скорбь и страсть, Как здесь, и даже Там та же мировая спесь”.
Б. Паскаль писал о бесконечности: “Я вижу со всех сторон только бесконечности, которые заключают меня в себе как атом; я как тень, которая продолжается только момент и никогда не возвращается. (И книги А. Ф. Лосева “Эстетика возрождения”, М., “Мысль”, 1982г. стр. 549).
Вариациями на тему бесконечность являются отрывки стихотворений таких поэтов и ученых, как римского поэта и философа Тит Лукреция Кара.
“Нет краев у нее, и нет ни конца, ни предела, И безразлично, в какой ты находишься части Вселенной. Где бы ты не был, везде, с того места, что ты занимаешь, Все бесконечной она остается во всех направленьях”.
Низами – среднеазиатский поэт вопрошал:
“Разве в мире бесконечном направленье есть? Разве далям бесконечным измеренье есть?”
Джордано Бруно писал:
“Кристальной сферы мнимую природу, Поднявшись ввысь, я смело разбиваю И в бесконечность мчусь, в другие дали. Кому на горе, а кому в отраду, - Я Млечный путь внизу вам оставляю...”
Немецкий поэт 18в. Альберт фон Галлер утверждал:
“Нагромождаю чисел тьму, Мильоны складываю в гору, Ссыпаю в кучу времена, Миров бесчисленных просторы. Когда ж с безумной высоты Я на тебя взгляну, то ты - Превыше не в пример Всех чисел и всех мер: Они лишь часть тебя”.
И, наконец, М. В. Ломоносов восклицал:
“Открылась бездна, звезд полна, Звездам числа нет, бездне – дна”.
И здесь уместно вставить слова Максимилиана Волошина:
“Когда уйду я в бесконечность, То мне откроется она, Так ослепительно ясна, Так беспощадна, так сурова, И звездным ужасом полна”.
Иллюстрациями этого понятия могут служить и некоторые замечательные графические работы известного голландского “математического графика”, художника М. К. Эшера (об этом уже начинали говорить выше). В этих работах Эшер, умело опираясь на математические конструкции,применяемые в алгебре и геометрии, подчеркивает несовершенство и ограниченность нашей геометрической интуиции.
Именно глубоким проникновением в природу геометрической бесконечности и объясняется сильное воздействие на зрителя “математических работ” Эшера.
На полотне можно изобразить лишь иллюзию бесконечности, но не саму бесконечность. Рассмотрим гравюры Эшера.
Гравюра “Все меньше и меньше” представляет собой первую попытку изображения бесконечности. При приближении к центру окружности фигурки, заполняющие плоскость, уменьшаются, каждая последующая фигурка занимает площадь вдвое меньшую, чем предыдущая: в центре площадь их становится бесконечно малой, а количество бесконечно большой величиной. Такая конструкция является фрагментарной, т. к. она позволяет расширение новыми все более увеличивающимися фигурами.
Избежать фрагментарности и представить бесконечность во всей ее полноте внутри четко очерченной границе позволяет лишь метод, обратный только что рассмотренному.
Это такие гравюры как “Круговой предел 1, 2, 3”
В круговом пределе 3 вдоль каждой цепочки сохранена однородная ориентация фигур, рыбки плывут вереницей по дугам от края до края гравюры и так, что чем ближе к центру, тем фигуры становятся больше. Каждая цепочка подобна траектории ракеты, которая взмывает с одной из точек окружности и исчезает на противоположной стороне. При этом ни одна из фигурок цепочки не достигает граненой линии, за пределами которой “абсолютное ничто”.
Но сферическая вселенная и не может существовать без охватывающей ее пустоты не только потому, что понятие “внутри” предполагает понятие “снаружи”, но и потому, что в этом “ничто” воображаемые, но геометрически точно определенные центры дуг, образующие структуру сферического мира.
Представим, что с нами разговаривает Эшер. Подслушаем его “Я часто слышу, что ученые говорят: “Наша вселенная безгранична”, и я не спорю, я просто беру карандаш и рисую... Я слышу она искривлена, но и это вообразить мне под силу... Вот с замкнутостью нашей вселенной, о которой прожужжали мне уши друзья-физики, мне пришлось потруднее, но и тут я справился, кое-что нарисовал (“Картинная галерея”)
Да немало я потрудился, чтобы представить замкнутость... но зато я теперь убедился, что глаз и рука могут создать и объяснить все на свете, даже бесконечность не пугает их...”
Работы Эшера можно демонстрировать, когда говорим о симметрии, о трехмерном пространстве, при изучении правильных многогранников и т.д. и т.п.
Об Эшере и его работах хочу сказать словами К. Маркса:
“Воображение — это великий дар, так много содействовавший развитию человечества”.
Воображение и точные расчеты, интуиция и чувство красоты помогли Праксителю и Иктину построить и Парфенон.
Парфенон кажется прямоугольным, но в нем не найдешь и двух линий, которые в действительности были бы параллельными, хотя они и кажутся нам таковыми. Его 72 колоны наклонены друг к другу, и если мысленно их продолжить, то все линии пересекутся в одной точке, на высоте около 8 км над землей.
В математике много романтики, но никогда не следует забывать о том, что изучение её – это не сплошной праздник, что любое научное творчество – это труд, труд, о котором часто без преувеличений можно сказать, что он каторжный. Гений – это прилежание, лишь один процент вдохновения и 99% потения.
Я хочу закончить свое выступление словами В. Брюсова:
“Когда вникаю я, как робкий ученик, В твои спокойные, обдуманные строки, Я знаю – ты со мной! Я вижу строгий лик, Я чутко слушаю великие уроки”.
P.S. Материриал об Анатолии Тимофеевиче Фоменко можно найти на сайте http:|| Anatoly-fomenko.com
Материал для демонстрации картин М.К. Эшера можно найти в альбоме: М.К.Эшер, Графика TASCHEN\АРТ - Родник, 2001, где предисловие и аннотации написаны самим автором. Некоторые описания картин из этой книги даю в приложении.



Приложение (описание картин)
Иллюстрации
xn--i1abbnckbmcl9fb.xn--p1ai
Вечность бытия и непобедимость бесконечности жизни!: volna888
Отзыв на картину из альбома Григория Грабового «Проявления Вечности» (стр. 58, том 1)

Картина, изображающая зимнее время года, выполнена в технике «Перо и чернила», очень древней технике.
На переднем плане видны два рядом стоящих изогнутых дерева, стволы которых абсолютно белые, заснеженные. Верхний контур деревьев прорисован черным цветом. Ещё одно дерево наклонилось к двум первым, переплетаясь своими ветвями. А за ними, сквозь редеющие обнаженные деревца, проглядывается силуэт жилого дома. Как же хорошо, выйдя на его балкон, любоваться окружающей тебя дивной природой!
На картине можно увидеть разные лица: мужские и женские, детские, различаются мордочки и фигуры животных, новогодняя ёлочка в снежных гирляндах и сказочные персонажи. Также привлекает внимание бездонность картины. Чем дольше на неё смотришь, тем больше приходит информации о вечном развитии, вечности жизни. Поражает объёмность пространства картины. Будто ты находишься внутри изображения и можешь рассмотреть каждый предмет в отдельности, дотронуться до веток деревьев и кустов. Картина оживает! И ты сливаешься с ней, ясно осознавая вечность бытия и непобедимость бесконечности жизни!
Сейчас зима. И когда смотришь в окно, идёшь по улице или гуляешь в парке, то невольно воспринимаешь действительность через призму этой картины и находишь области вечности вокруг себя. В преддверии Нового Года и Рождества Христова эта картина даёт особое состояние наполненности любовью, светом, радостью, верою в прекрасное будущее всего мира.
Я порекомендовал бы своим родным и близким, друзьям и знакомым не только эту, но также и другие картины автора из замечательного двухтомника «Проявления Вечности». Все картины в альбоме Григория Петровича Грабового несут позитивную информацию, добрые чувства, расширение сознания, радость восприятия действительности и являются чудесным подарком всем нам.
Андрей Ершов, декабрь 2013 года.
Art Gallery of Grigori Grabovoi – http://art.ggrig.com/
Книги Григория Грабового в международном интернет-магазине Amazon.com по ссылке:
http://www.amazon.com/s/ref=nb_sb_noss?url=search-alias%3Dstripbooks&field-keywords=grabovoi&rh=n%3A283155%2Ck%3Ag
Книги в вариантах: Kindle Edition – электронный, Paperback – бумажный.
volna888.livejournal.com
Татуировка знак бесконечность - значение, эскизы тату и фото
Татуировка знак бесконечность относится к самым простым эскизам для нанесения на тело, но при этом может нести в себе глубокий смысл, ведь сама по себе бесконечность – это не просто математический символ, а по-настоящему магический знак. Эскизы татуировки знака бесконечность рисуют не только в виде простой повернутой восьмерки, но и в самых разных вариантах с добавлением других символов или надписей.
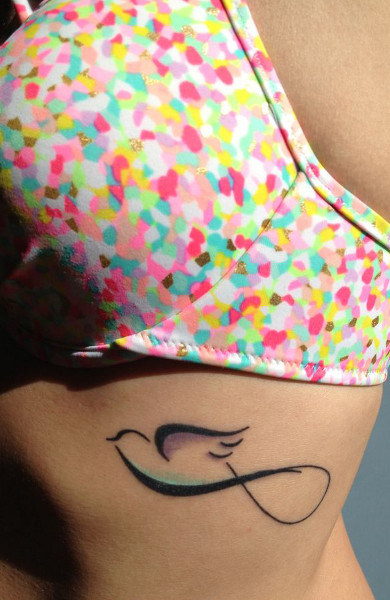

Происхождение этого знака связано вовсе не с математическими науками, как думают многие. Впервые этот символ был использован в наскальных гравюрах на территории Тибета, и изображал змею, кусающую саму себя за хвост. Согласно легенде, этого змея звали Уроборос, и главным его желанием было проглотить самого себя, однако длина его тела постоянно увеличивалась и чем больший кусок он пытался съесть, тем больше отрастало вновь. И эти попытки продолжались целую вечность. Таким образом этот знак стал символизировать объединение начала и конца.

Значение татуировки бесконечность – это желание человека жить без каких-либо ограничений, поскольку сам знак бесконечности указывает на невозможность поставить границы. Также такая татуировка может означать постоянный рост, непрекращающийся процесс саморазвития, вечное стремление двигаться вперед и не стоять на месте. Такой рисунок для тату часто выбирают для себя уверенные в себе люди и представители творческих профессий.

В теологии спираль бесконечности означает неограниченность и невозможность познать всё, вечное стремление к постижению бога и отсутствие возможности осуществления этого. Философская наука связывает этот символ с неизмеримостью времени и пространства, говорит о бесконечности природы и безграничности ее творческой силы.


Чаще всего в эскиз татуировки знака бесконечность ее обладатель вкладывает свой особый смысл. Для кого-то этот знак может означать бесконечную любовь или пожизненное одиночество, а кому-то этот символ служит напоминанием о прошлом и будущем.
Многие выбирают для себя такую тату, вкладывая в нее смысл невозможности познания нашего мира, вечности бытия и несчетности возможных перерождений. Часто татуировку бесконечность делают влюбленные пары, подтверждая таким образом бесконечную любовь и верность друг другу.

Татуировка бесконечность будет уместно смотреться на любой части тела, однако чаще всего ее можно встретить на запястье.
Видео татуировки бесконечность
А ниже представлены фото татуировок с изображением знака бесконечность от разных мастеров.
Фото татуировок бесконечность
uniquetattoo.ru









