Музей ЧерномырдинаПознавательный ресурс о культуре, науке и искусстве. Лестницы картина эшера
Мориц Корнелис Эшер: И тайное станет явным… | КУР.С.ИВ.ом
Автор статьи: Сергей КурийРубрика «Прочие статьи»
«Математики открыли дверь ведущую в другой мир, но самивойти в этот мир не решились. Их больше интересует путь,на котором стоит дверь, чем сад, лежащий за ней».(М. К. Эшер)
Когда я учился в первом классе, мне в руки попал один болгарский журнал. На одной из его страниц была напечатана удивительная картинка, где жутковатые хамелеоны томились в тисках… правильного многоугольника. В то время я мало интересовался именами художников, но саму картинку сохранил. Через какое-то время к ней добавилась обложка из журнала «Знание — сила», на которой цепочка муравьев совершала свой бесконечный путь по знаменитой ленте Мебиуса. У этих зоогеометрических фантасмагорий, поразивших мое юное воображение, оказался один и тот же автор — Мориц Корнелис Эшер. Так для меня открылась новая Страна Чудес, и я узрел невозможное.
Два автопортрета Морица Корнелиса Эшера: плоский и отраженный в сфере.
Тяга к падению и идеальный бутерброд
«Если бы вы только знали, какие видения посещают меня в ночной тьме…Иногда моя неспособность сделать их зримыми буквально сводит меня с ума.По сравнению с этими мыслями каждая отдельная гравюра или рисунок —это полная неудача, толькомельчайшая частица необъятного целого».(М.К.Эшер)
Голландский мальчик Мориц Корнелис Эшер (род. 1898 г.) с детства был немного странным. Бесцветный, замкнутый и заикающийся, он плохо учился и был подвержен двум маниям. Первую можно назвать «тягой к падению» — все вертикальные, устремляющиеся ввысь формы, имели для парня пугающую и одновременно восхитительную притягательность. Второй странностью маленького Эшера было построение «безупречного бутерброда». Однокашник будущего художника вспоминал, как тщательно укладывал Мориц на хлеб кусочки сыра и колбасы с целью получить «идеальное покрытие». Все эти геометрические мании закончились тем, что отец Морица однажды обнаружил рисунок своего сына, на котором был изображен… квадратный круг.Удивительный дар юноши был истолкован не совсем верно, и Морица послали учиться на архитектора. Однако вскоре он перевелся в класс графического дизайна. С тех пор основной художественной формой Эшера станет гравюра.
«Вавилонская башня».
По окончании учебы Эшер отправляется путешествовать по Италии и Испании, чтобы познакомиться с работами великих мастеров. Несмотря на то, что ранние картины самого Эшера были вполне натуралистичны, они уже полны неподражаемой гармоничной красотой и настоящей магией («Три мира», «Капля росы», «Лужица» и др.).
«Капля росы».
Мастер иллюзий
«Рисовать — значит обманывать».(М.К.Эшер)
В 1938 году Эшер практически перестает рисовать натуру. Его целиком захватывают странные «внутренние» картины, являющиеся к нему в озарениях и снах.Еще в 1936 году, посещая в Гранаде дворец Альгамбра, построенный арабами, художник был до глубины души потрясен мусульманскими мозаиками и орнаментами, их «колоссальной сложностью и математическо-художественным смыслом». И Эшер с той же энергией и фантазией, с которой когда-то складывал «идеальный бутерброд», переходит к составлению бесчисленных мозаик. Известно, что в мусульманском искусстве запрещено изображать живых существ. Эшер мусульманином не был (он вообще был атеистом), поэтому его мозаики заполнили, непостижимо слитые в единое целое, повторяющиеся фигурки демонов и ангелов, рыб и птиц. Никто до Эшера не осмеливался на столь сложный и дерзкий эксперимент! Сам художник называл деление плоскости «самым богатым источником своего вдохновения».
М.К.Эшер:«Иногда, когда я рисую, мне кажется, будто я медиум, находящийся во власти существ, порожденных моим же воображением. Они словно сами избирают, в каком виде им появиться… Линия, разделяющая две смежные фигуры, выполняет двоякую функцию, и провести такую линию чрезвычайно сложно. По обе стороны от нее обретает зримую форму то, что ранее существовало лишь в воображении. Но ни человеческий глаз, ни человеческий разум не могут одновременно созерцать две вещи, поэтому происходит быстрое и непрерывное переключение внимания с того, что находится по одну сторону линии, на то, что находится по другую сторону от нее. Но, вероятно, именно в этой трудности и кроется движущая пружина моего упорства».
В безумно сложных мозаиках Эшера трудно с первого раза заметить, что все они построены строго геометрично и имеют трех-, четырех- или шестинаправленную симметрию, благодаря чему сохраняют свойство заполнения плоскости без перекрытий и щелей.
Брат Морица, геолог по профессии, увидел в этих мозаиках наглядный материал для кристаллографии (наука о строении и симметрии кристаллов). Эшер решил подкрепить свою интуицию теорией, и в 1960-м году его лекциям по кристаллографии уважительно внимали профессора Кембриджа. А спустя пять лет Международный союз кристаллографов даже издает книгу «Симметрические аспекты периодических рисунков М. К. Эшера», где на 41-ом орнаменте демонстрируются все плоские кристаллографические группы.
Второй эксперимент Эшер решил проделать над… пространством. И добился не менее восхитительных и пугающих успехов. Падение прекрасно, ужасно приземление. И художник творит мир, в котором падение может длиться бесконечно. Его рыбки непрерывно уменьшаются, удаляясь от центра круга, поэтому не в силах вырваться за его границы. Бесконечность, имеющая предел — каково? Конечно, математиков самим этим фактом не удивишь, но одно дело — формулы и графики, а другое — вполне наглядные рыбки!
По поводу своей картины «Круговой предел» Эшер шутил:
«На самом деле этот вариант надо бы написать на внутренней поверхности полусферы. Я предложил его папе Павлу, чтобы он распорядился украсить таким образом внутреннюю часть купола собора святого Петра. Представьте себе бесконечное число крестов, висящих у вас над головой! Но папе идея не понравилась».
С пространством на картинах художника творятся самые настоящие чудеса: оно вспухает, причудливо изгибается и замыкается на самом себе.
«Балкон».
По замкнутой лестнице Эшера можно спускаться (или подниматься) бесконечно. Его вода может все время течь по спуску и тем не менее идти по кругу, зримо воплощая мечту изобретателей «вечного двигателя». В его квадрате можно сразу увидеть и внешнюю и внутреннюю сторону. Его юноша в картинной галерее может созерцать картину и… одновременно находиться в ней сам. И наоборот — миры могут существовать рядом, но никогда не встречаться.
Эшер писал о картине «Дом лестниц»:
«…верхняя половина литографии представляет зеркальное отражение нижней. Верхний пролет лестницы, по которому существо ползет вниз, слева направо, дважды представлен в зеркальном повороте — один раз в середине и один раз + в нижней части листа. На лестнице, в правом верхнем углу, мы не отличим поднимающихся от спускающихся: оба ряда движутся бок о бок, только один ряд ползет вверх, а другой — вниз».
«Дом лестниц».
Если нарисованные на двумерной плоскости фигуры мы способны воспринимать трехмерными, то почему бы трехмерное пространство не изобразить так, как будто мы смотрим на него из четвертого измерения? Можно ли изобразить невозможное? Эшер мог. Если итальянские мастера Возрождения изобрели перспективу, то голландский художник довел ее до абсурда. Дивные безумные пространственные построения, вспыхивающие в мозгу Эшера, воплощались, сводя с ума теперь его зрителей.
«Магическое зеркало». Из ниоткуда — в никуда.
В математике — двоечник, в искусстве — сухарь?
«Он слишком умозрителен, слишком философичен; этомумолодому человеку не присущи порывы и спонтанные движения,он — художник в очень незначительной степени».(докладная записка одного из учителей Эшера)
«…Он показывает совершенно новые отношения междуточками, поверхностями и пространством, междупричиной и следствием, возникающими в его гравюрах, хотяи странными, но, по-видимому, вполне возможными, мирами».(А. Флокои)
Меня с детства вводило в недоумение распространенное противопоставление разума и чувств, фантазии и реальности, науки и искусства, «физиков» и «лириков». Какое может быть противопоставление, если всё это не только легко уживалось в моей голове, но и взаимодействовало, подпитывая друг друга? Рождение ребенка, казалось мне не меньшим чудом, чем хождение по воде, а математические и физические теории оказывались порою причудливее самой изощренной фантазии.Впрочем, так считали далеко не все. Даже тесть Эшера с обывательским самодовольством шутил, что у зятька лучше всего получаются чертежи складских помещений. Недалеко от тестя ушли и профессиональные критики. Строгие и умозрительные работы Эшера обвинялись искусствоведами в сухости, просчитанности и излишней интеллектуальности. Поразительно, но в большинстве художественных каталогов и работ по истории живописи творчество этого геометрического гения до сих пор игнорируется!
Корнелиус Ван Шаак Рузвельт:«Чарльз Сноу отметил поистине странный факт, что искусство XX века так мало усвоило достижения науки XX века. Это наблюдение дало ему еще одно доказательство того, что наша цивилизация распалась на две различных культуры. Так же, как ранее Леонардо да Винчи, Эшер своим особым способом пытается уменьшить этот разрыв, и в этом, вероятно, главная причина его популярности не только среди молодых, но также и среди вполне уже зрелых ученых и инженеров. И когда критик с раздражением заявляет, что он ни во что не ставит Эшера, ему можно напомнить подпись под одной забавной карикатурой: «Они все идут туда! Надо бы и мне поторопиться, поскольку я их лидер».
М.К.Эшер: «Я часто ощущаю бОльшую близость к математикам, чем к коллегам-художникам. …Я играл, выражая себя в образах, учитывающих возможности представления. Все, что есть на моих картинах, — сообщения о моих открытиях …Все мои произведения — это игры. Серьезные игры. Я просто пытаюсь сложить маленьких зверушек вместе — я не нахожу, что это легко, но я получаю невероятное удовольствие, находя способ соединить их. Меня забавляют все вопросы, которые возникают, когда я работаю. Эти вопросы дразнят меня, и мое самое большое удовольствие — это понять о чем они, а затем найти ответы на них. Потом я делаю оттиск, чтобы другие смогли разделить мою радость. Вы называете это математикой?».
«Узы союза». Рассматривая подобные картины Эшера действительно трудно поверить, что он не любил сюрреализм.
Надо отметить, что Эшер никогда и не отвергал интеллектуальность своего творчества. Тем не менее, художника постоянно сравнивали с сюрреалистами, искали в его работах мистический смысл, а молодежь 1960-х вообще сделала их знаменем «психоделлической» культуры.2 Весь этот нездоровый ажиотаж изрядно раздражал Эшера.
М.К.Эшер:«Однажды мне позвонила одна дама: «Господин Эшер, я очарована вашим искусством. В ваших «Рептилиях» представлена реинкарнация». Я ответил: «Мадам, если вы это видите, пусть это будет так».
Эшер не раз заявлял, что никакого отношения к сюрреализму не имеет, его задача не загадывать неразрешимые загадки, а разгадывать их. И действительно, даже в самых причудливых картинах художника есть своя логика и гармония. Логика — это тоже искусство.
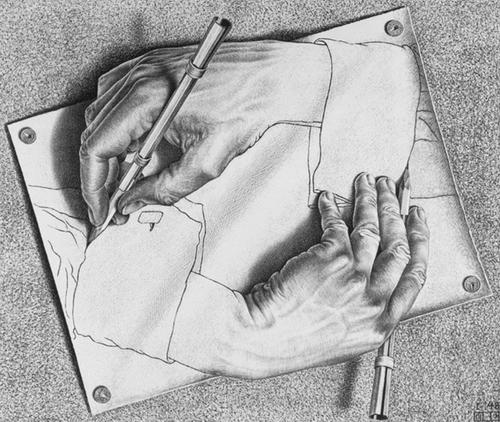«Рисующие руки». Интересно, что писал художник правой рукой, а рисовал левой.
Поэтому не удивительно, что обойденные искусствоведами, картины Эшера были с восхищением приняты в математических кругах. Математика всегда стояла особняком от других — «естественных» — наук, ибо, как и философия, имела дело с идеальными и абстрактными категориями (помните надпись на дверях платоновской Академии — «Негеометр да не войдет сюда»). Ну, скажите, где Вы видели в жизни ПРАВИЛЬНЫЙ многоугольник, НАСТОЯЩУЮ точку (объект, не имеющий размеров), или искривленное трехмерное пространство?Всемирная слава голландца началась в 1951 году после публикации его работ в трех журналах: «Time», «Life» и «Studio». А в 1954 году выставку Эшера приурочили к Международному математическому конгрессу. Нобелевский лауреат Чен Нин Ян с помощью гравюры «Всадник» даже пытался объяснять принцип симметрии в квантовой механике. Такая любовь математиков и физиков весьма озадачила Эшера, так как он считал себя в этих науках полным профаном. Когда геометр Г. Кокстер пригласил художника на свою лекцию о глубоком математическом смысле эшеровских рисунков, тот признался, что почти ничего в ней не понял…
М.К.Эшер:«Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен».
Слава Эшера росла, как снежный ком. Он получает королевскую награду, его посвящают в рыцари, в 1971 году выходит книга «Мир Эшера»…Но слава и деньги практически не меняют ни характер самого художника, ни его, более чем скромного, образа жизни. Он по-прежнему живет затворником в голландском городке Баарн. В 1968 году его жена покидает нелюбимую Голландию и возвращается в Швейцарию. Но художник уже стар и болен, он почти ни с кем не общается и его ждет только одно путешествие… Последним видением явленным в мир стала картина «Змеи» (1969 г.). В 1972 году в одной из лютеранских больниц дух Морица Корнелиса Эшера покидает наш евклидовый мир и исчезает в самой непостижимой бесконечности.
«Три мира».
_________________________________________________
ПРИЛОЖЕНИЕ: «Галерея Морица Эшера»:
«Бельведер»
СПРАВКА:Бельведер (в переводе с итал. «прекрасный вид») — постройка, сооруженная исключительно для того, чтобы из нее любоваться красотой вида, или башенку, возведенную с той же целью над крышей дома или дворца.
М.К.Эшер:«Слева, на переднем плане, лежит лист бумаги с чертежом куба. Места пересечения граней отмечены двумя кружками. Какая грань впереди, какая позади? В трехмерном мире невозможно увидеть переднюю и заднюю стороны одновременно, поэтому их не возможно изобразить. Однако есть возможность нарисовать предмет, передающий иную реальность, если смотреть на него сверху и снизу. Сидящий на скамейке юноша держит в руках именно такое абсурдное подобие куба. Он задумчиво разглядывает этот непостижимый предмет, оставаясь безразличным к тому, что бельведер за его спиной выстроен в том же невероятном, абсурдном стиле. На полу нижней площадки, то есть внутри, стоит лестница, по которой взбираются двое. Однако, достигнув верхней площадки, они снова окажутся снаружи, под открытым небом, и снова им придется входить внутрь бельведера. Удивительно ли что никому из присутствующих нет дела до заключенного, который просовывает голову между прутьями тюремной решетки и оплакивает свою судьбу?»
«Метаморфозы»
«Звёзды»
Именно с этой гравюры началось моё знакомство с творчеством Эшера.Здесь художник разрабатывает излюбленную тему правильных многоугольников. Изображенные звездчатые фигуры получены в результате объединения тетраэдров, кубов и октаэдров. Попавшие в геометрические клетку, хамелеоны придают гравюре эффект неожиданности..
«Двойной астероид»
М.К.Эшер:«Два правильных тетраэдра, пронизывающих друг друга, плывут в пространстве, как астероид. Темный тетраэдр населен людьми, преобразовавшими его в город с домами, мостами и дорогами. Светлый тетраэдр остался в своем естественном состоянии, с поросшими растительностью скалами и доисто-рическими животными. Итак, два небесных тела составляют единое целое, но они не имеют понятия друг о друге»
«Относительность»
М.К.Эшер:«Три силы тяжести направлены перпендикулярно одна другой. Три земные поверхности прорезают друг друга под прямым углом, и каждая населена человеческими существами. Обитатели двух разных миров не могут ходить, сидеть или стоять на одном и том же полу, поскольку у них разные представления о горизонтали и вертикали. Однако они могут пользоваться одной и той же лестницей. Мы видим как наверху два человека идут рядом по лестничным ступенькам будто бы в одном направлении, — тем не менее один движется вверх, а другой — вниз. Контакт между ними невозможен, так как они живут в разных мирах и не подозревают о существовании друг друга».
«Рептилии»
М.К.Эшер:«На раскрытой странице альбома — мозаика из зооморфных форм. Одной из рептилий надоело лежать рядом с неподвижными сотоварищами, поэтому она спускает переднюю ногу с края книги и вступает в реальную жизнь. Вползает на толстый переплет книжки по зоологии и проделывает трудный путь наверх. Коротко чихнув, усталое, но довольное, она переползает через пепельницу, спускается на прежнее место, становясь вновь элементом мозаики».
«Поднимаясь и спускаясь»
М.К.Эшер:«Бесконечные лестницы, представляющие главный мотив этой картины, навеяны статьей Л.С. и Р. Пенроузов, напечатанной в «Британском журнале психологии» в феврале 1958 года. Прямоугольник внутреннего двора замкнут стенами здания, у которого вместо крыши —бесконечная лестница. Скорее всего, в этом доме живут монахи, приверженцы некой религиозной секты. Возможно, ежедневный ритуал предписывает им подниматься по ступеням несколько часов подряд. Кажется, если они устанут, им разрешается повернуть в обратную сторону и спускаться, вместо того. чтоб подниматься. Однако оба направления, хотя и выразительны, но одинаково бесполезны. Двое непокорных индивидов в этот момент отказываются участвовать в ритуале. Им это совершенно не нужно, но нет сомнения, что раньше или позже их заставят раскаяться в своем нонкомформизме».
СПРАВКА:Кстати, для бессмысленной работы в голландском языке есть выражение «монашеский труд» (как у нас «Сизифов»).
«Водопад»
М.К.Эшер:«Конструкция составлена из перекладин, положенных одна на другую под прямым углом. Следя глазами за всеми ее элементами поочередно, мы не заметили ни малейшего несоответствия между ними. Однако перед нами — совершенно невозможное целое, поскольку в интерпретации расстояния между объектом и наблюдателем возникают неожиданные изменения. Эта немыслимая конструкция трижды «вмонтирована» в картину. Падающая вода приводит в движение мельничное колесо и течет по наклонному зигзагообразному желобу между двумя башнями, возвращаясь к точке, где водопад начинается снова. Мельнику достаточно время от времени плеснуть туда ведерко воды, чтобы компенсировать испарение. Кажется, что обе башни одинаковой высоты; тем не менее, та, что справа, оказывается этажом ниже, чем башня слева».
«Картинная галерея»
М.К.Эшер:«Вариант темы литографии «Балкон»: увеличение в центральной части то есть растяжение пространства, изгибающегося по часовой стрелке вокруг незаполненного центра. Вход справа внизу ведет нас на выставку — в галерею с экспозицией гравюр на стенах и в застекленных витринах. Мы минуем посетителя, заложившего руки за спину, а за тем — юношу (слева внизу), который по крайней мере в четыре раза крупнее того, первого. Даже голова у него увеличена в объеме по сравнению с его правой рукой. На стене перед ним — последний лист графической серии, и он пристально разглядывает пароход, лодки, воду канала и дома на заднем плане. Затем его взгляд переходит слева направо, к многоярусному жилому массиву. Открытое окно, из которого выглядывает женщина, выходит прямо на покатую крышу выставочной галерее, и это возвращает нас к месту, откуда началось путешествие. Юноша воспринимает все это как двухмерные детали рассматриваемой литографии. Если же глаза захватят еще больше пространства, ему покажется, что он вошел в мир графического листа».
Эта одна из самых невероятных картин Эшера долгое время не давала ученым покоя своим белым пятном в центре. Считается, что картина должна продолжаться дальше внутрь по спирали, но художник не смог решить эту задачу. Ну что же? Ее решили за него. Доктору Хендрику Ленстра удалось продолжить галерею внутрь, где она снова повторяет саму себя.
У вас есть возможность это увидеть (!). Для этого нужно зайти на сайт http://escherdroste.math.leidenuniv.nl в раздел Animation и скачать два небольших анимационных ролика (которые во время просмотра обязательно надо зациклить). Легкий сдвиг по фазе обеспечен!
4 ВАРИАНТА ОГРАНИЧЕННОЙ БЕСКОНЕЧНОСТИ:
1) «Меньше и меньше»Ящерицы до бесконечности мельчают по направлению к центру.
2) «Круговой предел»А здесь рыбы мельчают по направлению к краю круга.
3) «Змеи»В этой картине уменьшение идет в двух направлениях: и к краям, и к центру.
4) «Водоворот»Рыбы вырастают из одной бесконечной спирали и исчезают в другой.
«Другой мир — II»
М.К.Эшер:«Интерьер кубического здания. Сквозь проемы сдвоенных арок в пяти видимых нам стенах видны три разных пейзажа. Через верхние арки вы можете смотреть вниз, на землю почти вертикально; в двух средних линия горизонта находится на уровне глаз; сквозь нижнюю пару арок можно любоваться звездами.Каждая плоскость этого здания, объединяющая надир, горизонт и зенит, исполняет тройную функцию. Например, задний план (в центре) служит стеной относительно горизонта, полом относительно вида, открывающегося из верхних арок, и потолком мы видим звездное небо.»
«Лента Мебиуса»
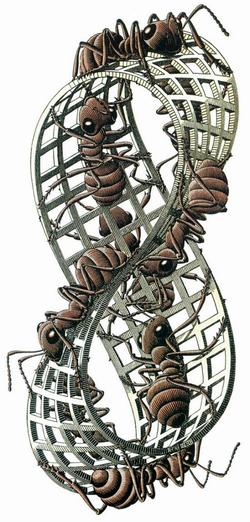
М.К.Эшер:«Замкнутая кольцеобразная полоса на первый взгляд имеет две поверхности: внешнюю и внутреннюю.Вы видите, как девять красных муравьев один за другим ползут и по той, и по другой. Тем не менее это полоса с односторонней поверхностью».
СПРАВКА:Лента Мебиуса — простейшая односторонняя поверхность, обнаруженная немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 г.Сделать такую ленту элементарно: вырежьте бумажную полоску, возьмите один ее край, разверните его на 180 градусов и приклейте к другому краю. Проводя карандашом линию по одной стороне ленты, вы обнаружите, что линия обрисовала ленту (и замкнулась) с обеих сторон, хотя вы не разу не переходили ее край.
Автор: Сергей КурийВпервые опубликовано в журнале «Время Z» №1 2008 (июнь)
www.kursivom.ru
Мориц Корнелис Эшер. Может ли геометрия быть искусством? Часть 1 | Культура
Когда я учился в первом классе, мне в руки попал один болгарский журнал. На одной из его страниц была напечатана удивительная картинка, где жутковатые хамелеоны томились в тисках… правильного многоугольника. В то время я мало интересовался именами художников, но саму картинку сохранил. Через какое-то время к ней добавилась обложка из журнала «Знание — сила», на которой цепочка муравьев совершала свой бесконечный путь по знаменитой ленте Мебиуса. У этих зоогеометрических фантасмагорий, поразивших мое юное воображение, оказался один и тот же автор — Мориц Корнелис Эшер. Так для меня открылась новая Страна Чудес, и я узрел невозможное.
Тяга к падению и идеальный бутерброд
«Если бы вы только знали, какие видения посещают меня в ночной тьме… Иногда моя неспособность сделать их зримыми буквально сводит меня с ума. По сравнению с этими мыслями каждая отдельная гравюра или рисунок — это полная неудача, только мельчайшая частица необъятного целого».(М.К. Эшер)
Голландский мальчик Мориц Корнелис Эшер (род. 1898 г.) с детства был немного странным. Бесцветный, замкнутый и заикающийся, он плохо учился и был подвержен двум маниям. Первую можно назвать «тягой к падению» — все вертикальные, устремляющиеся ввысь формы, имели для парня пугающую и одновременно восхитительную притягательность. Второй странностью маленького Эшера было построение «безупречного бутерброда». Однокашник будущего художника вспоминал, как тщательно укладывал Мориц на хлеб кусочки сыра и колбасы с целью получить «идеальное покрытие».
Удивительный дар юноши был истолкован не совсем верно, и Морица послали учиться на архитектора. Однако вскоре он перевелся в класс графического дизайна. С тех пор основной художественной формой Эшера станет гравюра.
По окончании учебы Эшер отправляется путешествовать по Италии и Испании, чтобы познакомиться с работами великих мастеров. Несмотря на то, что ранние картины самого Эшера были вполне натуралистичны, они уже полны неподражаемой гармоничной красотой и настоящей магией («Три мира», «Капля росы», «Лужица» и др.). К Италии Эшер настолько прикипел, что, женившись, решил поселиться в Риме. Уже в те времена талантливый голландец пользуется популярностью — так на крестинах сына Эшера присутствовали король Эммануэль и сам «дуче» Муссолини. Впрочем, когда по велению «почетного гостя» итальянских детей начали заставлять вступать в фашистскую организацию, художник не выдержал.
В 1935 году семья Эшера переезжает в Швейцарию, а с началом войны — в Голландию. Кроме расставания с любимой Италией, война принесет художнику и личное горе: в концлагере погибнет его учитель — еврей Самуэль Мескит. После ареста Мескета Эшер успевает посетить его дом и спасти картины учителя, переправив в музей Амстердама. Себе он оставит лишь один эскиз, на котором отпечаталась подошва фашистского сапога…
Мастер иллюзий
«Рисовать — значит обманывать».(М.К.Эшер)
В 1938 году Эшер практически перестает рисовать натуру. Его целиком захватывают странные «внутренние» картины, являющиеся к нему в озарениях и снах.
Еще в 1936 году, посещая в Гранаде дворец Альгамбра, построенный арабами, художник был до глубины души потрясен мусульманскими мозаиками и орнаментами, их «колоссальной сложностью и математическо-художественным смыслом». И Эшер с той же энергией и фантазией, с которой когда-то складывал «идеальный бутерброд», переходит к составлению бесчисленных мозаик. Известно, что в мусульманском искусстве запрещено изображать живых существ. Возможно, именно поэтому весь художественный потенциал арабского мира выплеснулся в головокружительных узорах-арабесках, витиеватость которых подчинялась строгой симметрии и периодичности.
Эшер мусульманином не был (он вообще был атеистом), поэтому его мозаики заполнили непостижимо слитые в единое целое, повторяющиеся фигурки демонов и ангелов, рыб и птиц. Никто до Эшера не осмеливался на столь сложный и дерзкий эксперимент! Сам художник называл деление плоскости «самым богатым источником своего вдохновения».
М.К.Эшер:«Иногда, когда я рисую, мне кажется, будто я медиум, находящийся во власти существ, порожденных моим же воображением. Они словно сами избирают, в каком виде им появиться… Линия, разделяющая две смежные фигуры, выполняет двоякую функцию, и провести такую линию чрезвычайно сложно. По обе стороны от нее обретает зримую форму то, что ранее существовало лишь в воображении. Но ни человеческий глаз, ни человеческий разум не могут одновременно созерцать две вещи, поэтому происходит быстрое и непрерывное переключение внимания с того, что находится по одну сторону линии, на то, что находится по другую сторону от нее. Но, вероятно, именно в этой трудности и кроется движущая пружина моего упорства».
Брат Морица, геолог по профессии, увидел в этих мозаиках наглядный материал для кристаллографии (наука о строении и симметрии кристаллов). Эшер решил подкрепить свою интуицию теорией, и в 1960-м году его лекциям по кристаллографии уважительно внимали профессора Кембриджа. А спустя пять лет Международный союз кристаллографов даже издает книгу «Симметрические аспекты периодических рисунков М.К. Эшера», где на 41-ом орнаменте демонстрируются все плоские кристаллографические группы.
Второй эксперимент Эшер решил проделать над… пространством. И добился не менее восхитительных и пугающих успехов. Падение прекрасно, ужасно приземление. И художник творит мир, в котором падение может длиться бесконечно. Его рыбки непрерывно уменьшаются, удаляясь от центра круга, поэтому не в силах вырваться за его границы. Бесконечность, имеющая предел — каково? Конечно, математиков самим этим фактом не удивишь, но одно дело — формулы и графики, а другое — вполне наглядные рыбки!
По поводу своей картины «Круговой предел» Эшер шутил: «На самом деле этот вариант надо бы написать на внутренней поверхности полусферы. Я предложил его папе Павлу, чтобы он распорядился украсить таким образом внутреннюю часть купола собора святого Петра. Представьте себе бесконечное число крестов, висящих у вас над головой! Но папе идея не понравилась».
С пространством на картинах художника творятся самые настоящие чудеса: оно вспухает, причудливо изгибается и замыкается на самом себе. По замкнутой лестнице Эшера можно спускаться (или подниматься) бесконечно (картина «Восхождение и спуск»). Его вода может все время течь по спуску и тем не менее идти по кругу, зримо воплощая мечту изобретателей «вечного двигателя» (картина «Водопад»). В его квадрате можно сразу увидеть и внешнюю и внутреннюю сторону (картина «Бельведер»). Его юноша в картинной галерее может созерцать картину и… одновременно находиться в ней сам (картина «Картинная галерея»). И наоборот — миры могут существовать рядом, но никогда не встречаться (картина «Двойной астероид»).
Если нарисованные на двумерной плоскости фигуры мы способны воспринимать трехмерными, то почему бы трехмерное пространство не изобразить так, как будто мы смотрим на него из четвертого измерения? Можно ли изобразить невозможное? Эшер мог. Если итальянские мастера Возрождения изобрели перспективу, то голландский художник довел ее до абсурда. Дивные безумные пространственные построения, вспыхивающие в мозгу Эшера, воплощались, сводя с ума теперь его зрителей.
P. S.: Всем заинтересовавшимся настоятельно рекомендую прочесть первый комментарий к этой статье.
shkolazhizni.ru
Творчество Эшера - HintFox
Возможно. Вы никогда не слышали этого имени. Но в любом случае вы обязательно видели его картины. И я увидел.
Художники, математики, естествоиспытатели – все, кто знаком с творчеством Эшера, были очарованы его картинами. Я не исключенье.
Морис Корнелис Эшер, нидерландский художник-график. Правильное произношение имени и фамилии Мауриц Корнелис Эсхер используется редко, отчасти ввиду неблагозвучности, отчасти из-за того, что нормы чтения голландского языка мало кому известны за пределами Нидерландов.
Морис родился 17 июля 1898 года в городе Леувардеке в семье инженера. Его родителей звали Джордж Арнолд Эшер и Сара Адриана Глейхман-Эшер. Морис был их младшим сыном (у него было четыре старших брата).
С 1912 по 1918 годы учился в средней школе. Хотя с раннего возраста он проявил способности к рисованию, его успехи в школе были весьма посредственными.
Голландский мальчик Морис Корнелис Эшер с детства был немного странным. Бесцветный, замкнутый и заикающийся, он плохо учился и был подвержен двум маниям.
Первую манию можно назвать «тягой к падению» - все вертикальные, устремляющиеся ввысь, формы, имели для парня пугающую и одновременно восхитительную притягательность. Многие картины пронизаны этой тягой к высоте и падению – к вертикали: «Вавилонская башня», «Относительность».
И вторая мания тоже преследовавшая его всю жизнь – это построение «безупречного бутерброда». Один из однокашников будущего художника вспоминал, как тщательно укладывал Морис на хлеб кусочки сыра и колбасы с целью получить «идеальное покрытие». Именно в необычные мозаики Эшера заложена эта тяга к идеальности – чтоб без просвета.
Все эти геометрические мании закончились тем, что отец Мориса однажды обнаружил рисунок своего сына, на котором был изображен квадратный круг.
И в 1918-1919 годах Эшера отправили учиться в Технический колледж в голландском городке Дельфт, но из-за плохого здоровья Морис не справился с учебным планом и был отчислен. В результате Эшер не получил высшее образование. Все еще в надежде получить диплом архитектора юный Эшер учится в школе архитектуры и орнамента в городе Гарлеме. Там он берет уроки рисования у Самюэля Джесерена де Месквита, оказавшего формирующее влияние на жизнь и творчество Эшера.
Как говорил сам художник: «Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти учение люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен». Это говорит человек, написавший одни парадоксы. Человек «абсолютно математически безграмотен», как он себя называет, жонглирует Платоновыми телами как жонглер булавами.
Правильные геометрические тела – многогранники – имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. Посмотрите на картину Эшера «Рептилии». Рептилии, выползающие из двумерного пространства, превращаются в трехмерные фигуры, переползающие через додекаэдр, и опять вползают в плоскость. В реалии невозможное явление, но за превращением каждого крокодильчика следишь, как завороженный.
На гравюре Мориса Эшера «Порядок и хаос» звездчатый додекаэдр, символ математической красоты и порядка, окружен прозрачной сферой. В ней отражена бессмысленная коллекция бесполезных вещей.
Наиболее интересными геометрическими работами являются гравюры «Звезды» и «Четыре тела». Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными и сквозь любой из них можно увидеть остальные. Гравюры и литографии Эшера - парадоксы из тематики «Этого не может быть никогда». Но это есть. Эшер сам заворожен и нас завораживает парадоксами. Он был очарован «невозможными фигурами».
Классической и одной из самых простых фигур является невозможный треугольник. В невозможном треугольнике каждый угол сам по себе является возможным, но парадокс возникает, когда мы рассматриваем его целиком. Стороны треугольника направлены одновременно и к зрителю, и от него, поэтому отдельные его части не могут образовать реальный трехмерный объект.
Эшер создал свою невозможную фигуру – это квадрат. И использует его в своих картинах для создания большей загадочности и абсурда.
Художник и, как настойчиво считают многие, математик Эшер прожил долгую и внешне достаточно спокойную, по большей части, жизнь. У него была любящая супруга, дети Но жил он не только этим миром. Большая часть сознания Эшера была отдана другим, невозможным в нашей реальности, мирам, единственное воплощение которых – его картины. Неправильно думать, что замысел картин рождался в голове гения. В процессе работы художник брал идеи из математических статей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость, «невозможных фигурах», логике трехмерного пространства. Парадокс и абсурдность невозможных фигур художник использует в своих работах. Невозможная лестница была первым невозможным объектом, который использовал Эшер в своем творчестве.
В реальности не существует лестницы, по которой можно подниматься, спускаться, как на его литографии «Восхождение и спуск». Прямоугольник внутреннего двора замкнут стенами здания, у которого вместо крыши бесконечная лестница, по которой идут на встречу друг другу люди
Если двигаться по лестнице по часовой стрелке, то мы будем постоянно подниматься, а если будем двигаться против часовой стрелки, то спускаться. Схема слева внизу показывает парадокс подъема.
Хотя может показаться, что такая конструкция невозможна в реальном мире, на самом деле невозможную лестницу можно представить в виде реальной модели. Секрет здесь кроется в том, что в реальной модели невозможной лестницы должен быть разрыв в районе правого угла, которого не видно, т. к. точка обзора выбрана намеренно, чтобы скрыть этот разрыв. Невозможные фигуры продолжают свое шествие по гравюрам художника-иллюзиониста Эшера.
«Водопад» - литография была напечатана в октябре 1961 года. В этой работе Эшера изображен парадокс – падающая вода водопада управляется колесом, которое направляет воду на вершину водопада. Водопад имеет структуру «невозможного» треугольника Пенроуза.
Рассмотрим упрощенную компьютерную модель. Конструкция составлена из трех перекладин, положенных друг на друга под прямым углом. Водопад работает как вечный двигатель. Перед нами картина, изображающая чертеж вечного двигателя! Но, как известно из школьного курса физики, вечный двигатель невозможен. Как же Эшеру удалось с такими подробностями изобразить то, чего в природе вообще не может быть?! При попытке соорудить двигатель согласно чертежу «обман» всплывает сразу – в трехмерном пространстве такие конструкции геометрически противоречивы и могут существовать только на бумаге, т. е. на плоскости, а иллюзия объема создается лишь за счет признаков перспективы (в данном случае – умышленно искаженных).
Развенчаем иллюзии и загадки Эшера. Так выглядит водопад в реальном мире. Совсем не завораживающе и не привлекательно. Нужны ли не интересные реалии. Они нас окружают. Любой парадокс, обман, иллюзию Эшера можно развенчать и объяснить, но интересно ли это. В познавательном смысле – да! Все в детстве хотели узнать, чем ходит будильник, и лезли его разбирать. Кроме разочарования этот разгром ничего не приносил. И все-таки иллюзия, как и надежда, - двигатель прогресса и красоты.
«Бельведер» Эшером был создан в реальном мире. На литографии изображен средневековый математик; мальчик, изучающий невозможный куб, люди, поднимающиеся по лестнице изнутри в наружу. Да, Бельведер выстроен в абсурдном стиле. А надо ли нам знать как правильно. Пусть Бельведер останется Бельведером Эшера, непознанный и загадочный с прямыми углами и параллельными колонами.
Вот он в реалии. Все соединено не по правилам геометрии трехмерного пространства или почти все. Эшер в своих работах все меняет, это выливается в метаморфозы. Постепенные качественные изменения приводят к изменению образа. Обыкновенному человеку сложно отследить эти изменения – переплетения, выливающиеся во что-то абсолютно новое и непредсказуемое.
Общепринято мнение, что математическое начало доминирует в творчестве Эшера. Он сам говорил: «Хотя я абсолютно несведущ в точных науках, мне иногда кажется, что я ближе к математикам, чем к моим коллегам – художникам». Мастер иллюзии интересовался всеми видами мозаик – регулярными и нерегулярными (периодическими и квазипериодическими), а также ввел собственный вид, который назвал «метаморфозами», где фигуры изменяются и взаимодействуют друг с другом. Во всех работах Эшера используется ассиметричная геометрия. Он один из немногих умел на холсте изобразить «метаморфозы», применяя к ним трансформации, которые в геометрии называются симметрия, отражение, смещение, параллельный перенос и другие.
Это самая большая картина художника размером 19 см на 39 м. В ней представлены 10 трансформаций. В них он ничего не доказывал, он выплетал орнамент, не задумываясь о теории относительности и кристаллографии. Его увлекало перетекание одной формы в другую: плоской – в объемную, неживой – в живую. «Оживающие орнаменты» Эшера дают полное представление о замысле художника: орнамент (кристаллическая решетка) постепенно нарушает свою строгую упорядоченность, превращаясь в живые существа. В отличие от реального физического процесса, в котором нарушение порядка увеличивает молекулярный хаос, у Эшера старый «неодушевлённый» порядок переходит в новый «одушевлённый».
Творчество Эшера проникло во многие сферы жизни: его произведения используют в качестве наглядных пособий ученые и психологи, его работы часто становятся иллюстрациями сложных модернистских романов, красуются на обложках пластинок популярных рок-групп, став неотъемлемой принадлежностью современности. Эшер не много не дожил до компьютерной революции (он умел 27 марта 1972 г. ), но сейчас многие компьютерные дизайнеры говорят, что Эшер предвидел компьютерную графику. Этому мастеру принадлежит особое место в истории мировой художественной культуры. Эшеру в своём творчестве удалось выявить связь искусства и науки. Художник рисовал те образы, которые возникали у него в голове, не задавая себе вопроса: «А зачем это? Для чего?». Мне кажется, он и сам не знал ответы на эти вопросы. Мало того, что это все математически корректно, это все еще и очень красиво.
Об Эшере можно говорить бесконечно, об его фракталах, которые он рисовал вручную, о его мозаиках, гравюрах, литографиях. Сам художник утверждал: «Все мои произведения – это игры. Серьезные игры».
www.hintfox.com
Морис Корнелис Эшер (1898-1972) - Кто здесь?
Convex and concave (Выпуклые и вогнутые). Литография, 1955.В Москве проходит выставка работ Эшера в рамках года Нидерландов в России. В нашей стране его работы можно было увидеть лишь однажды в Эрмитаже в 2003г, и мне посчастливилось там побывать. Шла я знать не зная, кто такой этот Эшер, а выходила раз и навсегда влюблённая в его работы :) В этот раз в Питере можно посмотреть только на факсимальные репродукции в Выставочном зале Центра книги и графики. Ну, а тем, у кого нет возможности побывать на выставках, предлагаю немного ознакомиться с удивительным творчеством Эшера.
Морис Корнелиус Эшер (17 июня 1898, Леуварден, Нидерланды — 27 марта 1972, Ларен, Нидерланды) — "Хотя я абсолютно несведущ в точных науках, мне иногда кажется, что я ближе к математикам, чем к моим коллегам-художникам" - нидерландский художник-график. Известен прежде всего своими концептуальными литографиями, гравюрами на дереве и металле, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического восприятия сложных трёхмерных объектов.Circle Limit IV (Циклический предел). Гравюра на дереве, 1960
Не буду описывать его биографию, ссылка есть внизу, и пропущу ранние периоды, да, и вообще много интересных работ пропущу, т.к. просто невозможно объять его всего за один раз и за один пост. Только интересные факты, сам Эшер и его произведения, оставившие у меня наибольшее впечатление. Т.е. очень субъективный взгляд.
Order and chaos (Порядок и хаос). Литография, 1950
Морис Эшер, как многие гении и до и после него, утверждал: «Все мои произведения — это игры. Серьезные игры». Однако в этих играх математики всего мира вот уже несколько десятилетий рассматривают абсолютно серьёзные, материальные доказательства идей, созданных с помощью исключительно математического аппарата, или оригинальные контрпримеры, бросающие вызов здравому смыслу. Их воспринимают как прекрасные иллюстрации к научным трактатам по кристаллографии, когнитивной психологии или компьютерной графики.
Reptiles (Рептилии). Литография, 1943.
С помощью работ Мориса Эшера можно объяснить такие математические понятия и термины, изучаемые в школе, как: параллельный перенос, подобие фигур, равновеликие фигуры, периодичность. А так же некоторые понятия не входящие в школьный курс математики. В этот список можно включить следующие термины: квазипериодичность, инфляция, дефляция, треугольники Робинсона, преобразование дуальности.
Moebius Strip II (Лента Мёбиуса II). Гравюра на дереве, 1963.
Однажды известный геометр Г. Кокстер пригласил Эшера на свою лекцию, посвященную математическому содержанию его гравюр и литографий. К взаимному разочарованию, Эшер не понял почти ни слова из того, о чем рассказывал Кокстер. «Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен».
Hand with Reflecting Sphere (Рука с зеркальной сферой). Литография, 1935.
Первая картина невозможной реальности, созданная Эшером на основе своих эскизов путешествия по Средиземному морю.
Still life and Street. Гравюра на дереве, 1937.
Тогда же он начинает интересоваться мозаиками и едет в Альгамбру для детального изучения мавританских мозаик, впоследствии он скажет, что это было для него "богатейшим источников вдохновения".
Metamorphosis I (Метаморфозы I). Гравюра на дереве, 1937
Позже в 1957 году в своем эссе о мозаиках Эшер написал:"В математических работах регулярное разбиение плоскости рассматривается теоретически... Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней".
Day and Night (День и Ночь). Гравюра на дереве, 1937.
Sky and Water I (Небо и вода I). Гравюра на дереве, 1937
Впечатление объемности целиком определяется нашей интерпретацией рисунка и порой бывает иллюзорно. В произведении «Три сферы» Эшер изобразил три плоских диска. Нижний диск лежит на столе. Средний перегнут под прямым углом вдоль диаметра. Верхний диск стоит вертикально на горизонтальной половине среднего диска.
Three Spheres I (Три сферы I). Резьба по дереву, 1947
При рассматривании этой гравюры в попытке объять пространство у меня начинает кружиться голова.
Other World (Другой мир). Резьба по дереву, гравюра на дереве, 1947Эшер: "Интерьер кубического здания. Сквозь проемы сдвоенных арок в пяти видимых нам стенах видны три разных пейзажа. Через верхние арки вы можете смотреть вниз, на землю – почти вертикально; в двух средних линия горизонта находится на уровне глаз; сквозь нижнюю пару арок можно любоваться звездами. Каждая плоскость этого здания, объединяющая надир, горизонт и зенит, исполняет тройную функцию. Например, задний план (в центре) служит стеной относительно горизонта, полом – относительно вида, открывающегося из верхних арок, и потолком – мы видим звездное небо.
В следующей литографии используется идея самовоспроизведения. Руки рисуют друг друга, создавая самих себя. При этом сами руки и процесс их самовоспроизведения неразделимы.
Drawing Hands (Рисующие руки). Литография, 1947.Эшер: "Лист бумаги прикреплен к доске кнопками. Правая рука делает на листе набросок манжеты с запонкой. Работа еще не закончена, но справа уже детально прорисована левая рука: она высовывается из рукава так реалистично, словно вырастает из плоской поверхности, и, в свою очередь, делает набросок другой манжеты, из которой, подобно живому, существу выползает правая рука".
А это Эшер изобразил себя с супругой.
Bond of Union. Литография, 1956.
И напоследок немного игры с пространством, самая любимая мною тема в творчестве Эшера. Могу бесконечно ходить по лесенкам, менять верх с низом и оказываться то внутри, то снаружи.
Up and Down (Вверх и вниз). Литография. 1947.Эшер: "В этой литографии одна и та же картина представлена дважды, но мы рассматриваем ее с двух разных точек. Верхняя часть – вид, который откроется наблюдателю, если он поднимется тремя этажами выше; нижняя часть – сцена, которую он увидит, стоя на земле, то есть на площадке, выложенной изразцовыми плитками. Подняв глаза вверх, он увидит этот же плиточный пол, повторенный как потолок в центре композиции, однако он в то же время служит полом для верхней сцены. Вверху плиточный повторяется вновь, на этот раз как настоящий потолок".
Relativity (Относительность). Литография, 1953.Эшер: "Три силы тяжести направлены перпендикулярно одна другой. Три земные поверхности прорезают друг друга под прямым углом, и каждая населена человеческими существами. Обитатели двух разных миров не могут ходить, сидеть или стоять на одном и том же полу, поскольку у них разные представления о горизонтали и вертикали. Однако они могут пользоваться одной и той же лестницей. Мы видим как наверху два человека человека идут рядом по лестничным ступенькам будто бы в одном направлении, – тем не менее один движется вверх, а другой – вниз. Контакт между ними невозможен, так как они живут в разных мирах и не подозревают о существовании друг друга".
Print Gallery (Картинная галерея). Литография, 1956
Описание Эшера: "Вход справа внизу ведет на выставку – в галерею с экспозицией гравюр на стенах и в застекленных витринах. Мы минуем посетителя, заложившего руки за спину, а затем – юношу (слева внизу), который по крайней мере в четыре раза крупнее того, первого. Даже голова у него увеличена в объеме по сравнению с его правой рукой. На стене перед ним – последний лист графической серии, и он пристально разглядывает пароход, лодки, воду канала и дома на заднем плане. Затем его взгляд переходит слева направо, к многоярусному жилому массиву. Открытое окно, из которого выглядывает женщина, выходит прямо на покатую крышу выставочной галереи, и это возвращает нас к месту, откуда началось путешествие. Юноша воспринимает это как двухмерные детали рассматриваемой литографии. Если его глаза захватят еще больше пространства, ему покажется, что он вошел в мир графического листа".
Belvedere (Бельведер). Литография, 1958Эшер: "Слева на переднем плане лежит лист бумаги с чертежом куба. Места пересечения граней отмечены двумя кружками. Какая грань впереди, какая позади? В трехмерном мире невозможно увидеть переднюю и заднюю стороны одновременно, поэтому их невозможно изобразить. Однако есть возможность нарисовать предмет, передающий иную реальность, если смотреть на него сверху и снизу. Сидящий на скамье юноша держит в руках именно такое абсурдное подобие куба. Он задумчиво разглядывает этот непостижимый предмет, оставаясь безразличным к тому, что бельведер за его спиной выстроен в том же невероятном, абсурдном стиле. На полу нижней площадки, то есть внутри, стоит лестница, на которую взбираются двое. Однако, достигнув верхней площадки, они снова окажутся снаружи, под открытыми небом, и снова им придется входить внутрь бельведера. Удивительно ли, что никому из присутствующих нет дела до заключенного, который просовывает голову между прутьями тюремной решетки и оплакивает свою судьбу?"
Ascending & Descending (Восхождение и спуск). Литография, 1960Эшер:"Бесконечные лестницы, представляющие главный мотив этой картины, навеяны статьей Л.С. и Р. Пенроузов, напечатанной в "Британском журнале психологии" в феврале 1958 года. Прямоугольник внутреннего двора замкнут стенами здания, у которого вместо крыши – бесконечная лестница. Скорее всего, в этом дому живут монахи, приверженцы некой религиозной секты. Возможно, ежедневный ритуал предписывает им подниматься по ступеням несколько часов подряд. Кажется, если они устанут, им разрешается повернуть в обратную сторону и спускаться, вместо того чтобы подниматься. Однако оба направления, хотя и выразительны, но одинаково бесполезны. Двое непокорных индивидов в этот момент отказываются участвовать в ритуале. Им это совершенно не нужно, но нет сомнения, что раньше или позже их заставят раскаяться в своем нонконформизме.".
Waterfall (Водопад). Литография, 1961Эшер:"В статье "Британского журнала психологии" Р. Пенроуз опубликовал чертеж треугольника в перспективе, копия которого воспроизводится здесь. Конструкция составлена из перекладин, положенных одна на другую под прямым углом. Следя глазами за ее элементами поочередно, мы не заметим несоответствия между ними. Однако перед нами – совершенно невозможное целое, поскольку в интерпретации расстояния между объектами и наблюдателем возникают неожиданные изменения. Эта немыслимая конструкция трижды "вмонтирована" в картину. Падающая вода приводит в движение мельничное колесо и течет по наклонному зигзагообразному желобу между двумя башнями, возвращаясь к точке, где водопад начинается снова. Мельнику достаточно время от времени плеснуть туда ведерко воды, чтобы компенсировать испарение. Кажется, что обе башни одинаковой высоты; тем не менее, та, что справа, оказывается этажом ниже, чем башня слева.".
А так могло бы выглядеть рабочее место художника (основано на его работах):
Ссылки:Здесь можно ознакомиться с его биографией, разделением работ по темам и исследованием белого пятна в середине литографии "Картинная галерея".На этом сайте ещё множество интересных работ, не поместившихся в пост.www.mcescher.com - официальный сайт и русская версия mcesher.ru (отсюда видео).
smeyashka.livejournal.com
Паркет глазами Эшера. - ... заметки на память
Текст взят:(с)«Уроки творчества: искусство и технология в школе», Сеть творческих учителей. (с) Солодуша Пётр Юрьевич(c) adenis
Из всех работ Эшера лучше всего известны его орнаменты (или мозаики, или тесселяция), то есть периодическое заполнение плоскости одинаковыми фигурами без их пересечений и щелей между ними. Разбивая плоскость на хитроумные комбинации контуров птиц, рыб, пресмыкающихся, млекопитающих и человеческих фигур, Эшер умело включает свои орнаменты в необычайные, подчас озадачивающие неожиданными решениями композиции.
Увлечение этим необычным делом началось для него с посещения в 1922 году мавританского дворца Альгамбры, в Гранаде, Испания, где он был очарован великолепными мозаиками, сделанными мастерами-маврами в четырнадцатом веке. Посетив дворец еще раз в 1936 году, Эшер испытал творческий толчок, который определил его увлечение на всю оставшуюся жизнь.
Впоследствии он сказал, что это было для него "богатейшим источником вдохновения". Позже в 1957 году в своем эссе о мозаиках Эшер написал:
"В математических работах регулярное разбиение плоскости рассматривается теоретически... Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней".
Судя по словам очевидцев, рисовать все новые и новые варианты разбиения плоскости на повторяющиеся элементы стало для художника настоящей манией. Достаточно сказать, что во время Второй Мировой войны, в окупированой Голландии, Эшер не рисовал почти ничего, кроме мозаик. В 1958 году художник опубликовал книгу "Регулярное разбиение плоскости", где свел вместе свои опыты такого рода.
Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. Нерегулярных вариантов разбиения плоскости гораздо больше. В частности в мозаиках иногда используются нерегулярные мозаики, в основу которых положен правильный пятиугольник. Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шестинаправленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей.
Орнаменты на стенах Альгамбры свидетельствуют о том, сколь искусны были испанские мавры в изобретении узоров, состоящих из периодических повторений конгруэнтных фигур. Но мусульманская религия запрещала мавританским мастерам использовать в орнаментах изображения живых существ: человека, животных, рыб и птиц, потому мусульманские орнаменты составлены из абстрактных геометрических фигур. Эшера очень занимала задача составления орнаментов, использующих в качестве повторяющихся элементов реальные изображения.
"Всадники" - это образец искусства регулярного разбиения плоскости, в котором Эшер преуспел, как никакой другой современный художник.
Из теории известно, что мозаики из одинаковых элементов могут быть созданы с использованием всего трех операций над элементами: переноса, поворота и отражения. Всего существует не много не мало, а семнадцать их вариантов (групп симметрий). Вот они все:
.Например, "Всадники" здесь - это вариант O1gg - зеркальный перенос.
Эшер узнал обо всем этом, прочитав в 1937 году работу профессора Полии, посвященную кристаллографии (рисунок оттуда), в которой он неожиданно для себя нашел новый источник вдохновения. Вооруженный теорией, художник за всю свою жизнь сделал 137 гравюр с мозаиками, а также бесчисленное количество рисунков, из которых мавританские всадники, скачущие настречу друг другу, стали, пожалуй, наиболее популярными.Эшер лишь немного не дожил до утверждения теории псевдокристаллов и «непериодических» кристаллов – можно только догадываться, на какие работы подвигли бы его эти теории…"Иногда, когда я рисую, мне кажется, будто я медиум, находящийся во власти существ, порожденных моим же воображением, — сказал как-то раз Эшер — Они словно сами избирают, в каком виде им появиться... Линия, разделяющая две смежные фигуры, выполняет двоякую функцию, и провести такую линию чрезвычайно сложно. По обе стороны от нее обретает зримую форму то, что ранее существовало лишь в воображении. Но ни человеческий глаз, ни человеческий разум не могут одновременно созерцать две вещи, поэтому происходит быстрое и непрерывное переключение внимания с того, что находится по одну сторону линии, на то, что находится по другую сторону от нее. Но, вероятно, именно в этой трудности и кроется движущая пружина моего упорства”.
О том, сколь многими способами фантастические орнаменты Эшера иллюстрируют различные аспекты симметрии, теории групп и кристаллографических законов, можно было бы написать целую книгу. Такая книга действительно была написана Каролиной Макгиллэври из Амстердамского университета. Называлась она "Симметрийные аспекты периодических рисунков M. К. Эшера” и была издана Международным союзом кристаллографов. В ней собраны репродукции 41 орнамента Эшера (многие из них—цветные).
"Среди окружающего нас нередко хаотического мира, — писал Эшер, — они служат непревзойденным по своей выразительности символом извечного стремления человека к гармонии и порядку. В то же время их совершенство вызывает у нас ощущение собственной беспомощности. Правильные многогранники совершенно лишены человеческого элемента. Их нельзя считать изобретениями человеческого разума, ибо они существовали в земной коре в виде кристаллов задолго до того, как на сцене появилось человечество. Что же касается сферических форм, то разве сама Вселенная не состоит из сфер?”
В XXI веке популярность художника необычно возросла. Его литографии, гравюры на дереве можно увидеть в кабинетах математиков и других ученых во всех уголках мира. С середины прошлого века без его гравюр не обходится ни одна «иллюстрированная» книга по математике, физике, топологии, не говоря уж о популярных изданиях! На сайтах в сети Internet мы увидели чашки, галстуки, часы и красивые ткани, украшенные паркетами Эшера. Последний «писк» моды футболки с рисунками орнаментов Эшера. Фигурные элементы мощения – брусчатые камни.
Попробуем разобраться, как Эшер создавал свои паркеты. Например, в основе паркета «Ящерицы» - правильный шестиугольник. Если внутри вырезается некоторый "кусочек" плоскости, то такой же надо добавить снаружи.
Некоторые «базовые» фигуры Эшера:
На рисунках 1-4 приведены фрагменты некоторых картин художника.
Рисунок 1. Фрагмент картины «Птицы».
Рисунок 2. Фрагмент картины «Рыбы».
Рисунок 3. Фрагмент картины «Две птицы» (1 вариант).
Рисунок 4. Фрагмент картины «Две птицы» (2 вариант).
Синим цветом выделены варианты геометрических фигур (квадрат, треугольник, ромб, параллелепипед), которые возможно послужили художнику основой для создания образов животных. Разноцветными стрелками отмечены те участки геометрической фигуры, которые нуждаются в параллельном переносе.
Фото 2. | Фото 3. | ||
Фото 4. | Фото 5. | ||
Фото 6. | Фото 7. | ||
Фото 8.
Геометрические преобразования и паркеты. Задания для учащихся 5-9-х классов.
«Корел», Эшер, «Фотошоп»…: тесселяции своими руками.
==============================================================Межгрупповой отбор формирует социум, а внутригрупповой его поддерживает
Колонии факультативно социальных пауков Anelosimus studiosus, обитающих на территории Северной Америки, состоят из смеси «мирных» и «агрессивных» самок, которые совместно охотятся и заботятся о коммунальном потомстве. Оба поведенческих фенотипа являются генетически обусловленными, то есть наследуются по классическому менделевскому типу. Новые колонии формируются выселяющимися дочерьми, но значительная часть колоний просто вымирает, не оставляя отпрысков. Такая ситуация благоприятствует действию группового отбора, который, как доказали авторы исследования, и формирует оптимальную структуру сообщества. Однако до сих пор оставалось неясным, какой же, собственно, механизм обеспечивает поддержание оптимального соотношения «мирных» и «агрессивных» в функционирующей колонии и в ее отводках. В новом исследовании авторы продемонстрировали, что особи избыточного фенотипа в колонии производят меньше яиц, чем особи дефицитного фенотипа. То есть структура внутри колонии поддерживается благодаря частотно-зависимому отбору, реализуемому через генетически обусловленные (наследуемые) механизмы саморегуляции в репродуктивной системе самок.
aazz-z.livejournal.com
Невозможного нет: Реальная лестница Эшера
Одним из основных направлений творчества великого голландского графика Мориса Эшера было изображение невозможных объектов. Замкнутые круговые лестницы, ведущие только вверх, самопересекающиеся квадраты и треугольники — Эшер по‑новому осмысливал трехмерное пространство, пытаясь передать на холсте свое видение геометрических парадоксов
Фигуры Рутерсварда
Развертка треугольника Пенроуза Перед началом сборки развертку необходимо наклеить на плотный картон. Линии сгиба (обозначены пунктиром) рекомендуется чем-нибудь продавить
Фигуры Рутерсварда
Мы не пытались повторить работы Эшера и его последователей, но поставили перед собой другую задачу, не менее интересную. В парижском музее La Cité des sciences et de l’industrie («Городок науки и техники») есть целый зал, заполненный невозможными фигурами Эшера из картона, дерева, стекла и глины. Их можно потрогать и удивиться тому, как зрительные иллюзии претворяются в жизнь. Собственно, этим мы и занялись — изготовлением невозможных фигур своими руками. Как оказалось, это не так и сложно. Главное — рассчитать пропорции и правильно начертить развертку. После этого вступают в дело ножницы и клей. Естественно, можно то же самое сделать из поролона, дерева или пластика. Но картонные фигуры отличаются тем, что с ними справится почти любой желающий. Самое интересное, что практически любую невозможную фигуру можно свернуть из бумажного листа формата A4. Нужно просто подумать и применить пространственное воображение. Удачи!
Фигуры Рутерсварда
За свою жизнь Оскар Рутерсвард создал несколько тысяч невозможных фигур. Большую часть он просто чертил, соблюдая правила перспективы, а затем грамотно заштриховывал. Некоторые же он превращал в полноценные картины, некоторые оставались в виде набросков. Почти каждую фигуру Рутерсварда кто-нибудь рано или поздно создавал в объеме. Кое-какие сделал в объеме и сам художник. Мы выбрали более или менее известные фигуры из великого множества работ шведа. Результат перед вами.
Большинство невозможных геометрических фигур очень просты и состоят из простейших геометрических объектов: параллелепипедов, кубов, цилиндров. Это дает воображению неограниченный простор в создании новых оптических иллюзий
Статья опубликована в журнале «Популярная механика» (№1, Январь 2010).www.popmech.ru
