Музей ЧерномырдинаПроект по внеурочной деятельности на тему: «Математика в живописи». Картины математические
Удивительная математическая живопись / Всё самое лучшее из интернета
ziza.qip.ru klikabol.com
Математика и живопись. Творчество Маурица Корнелиса Эшера
Поделиться статьей
Казалось, после Леонардо да Винчи, увлеченного решением геометрических задач, художники перестали видеть в «царице всех наук» искусство. Но спустя несколько столетий родившийся в 1898 году голландский художник Мауриц Корнелис Эшер попытался снова вернуть в живопись точность науки. Concepture публикует статью о творчестве художника.
Мориц Корнелис Эшер занимает особенное место в живописи XX века. В его работах нашел отражение самый широкий круг математических идей. Интересно, что в школе Эшер хуже всего занимался по рисованию и математическим дисциплинам. Да и начинал он впоследствии не как художник-математик, а как гравер, изображавший тонкости итальянских пейзажей. И только посетив Альгамбру, мавританский архитектурный ансамбль, Эшер, пораженный великолепием плиточных мозаик, решает поставить математику на службу искусству. Так начинаются его математические эксперименты в области живописи, которые чаще всего способны заинтересовать архитекторов, а не коллекционеров.
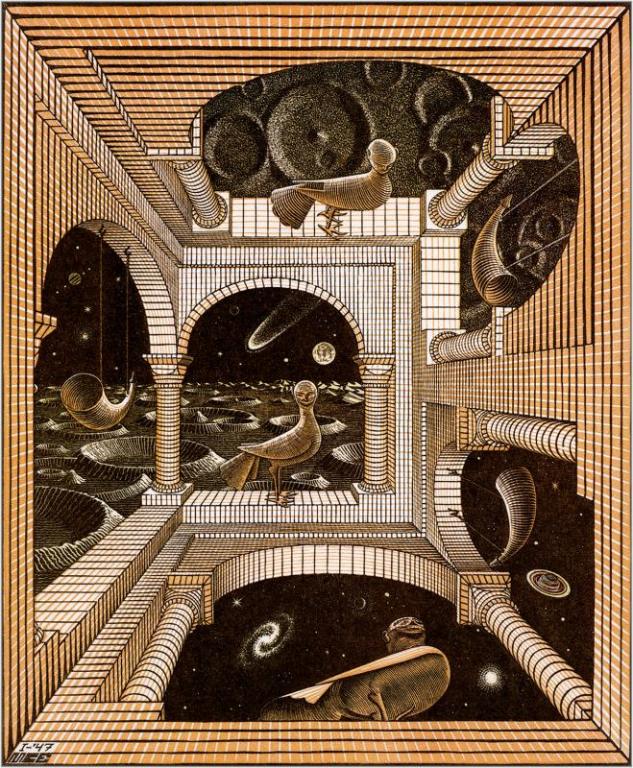
Как это не странно, вдохновение для создания своих картин Эшер черпал не из окружающего мира, а из научных трудов по кристаллографии и плоскостной симметрии. Поэтому и его творчество было всецело подчинено изображению абстрактных математических законов, их визуальной интерпретации. Больше всего Эшера привлекали манипуляции с плоскостями и трехмерное пространство. Плодами его художественно-математических опытов стали знаменитые картины «Относительность», «Водопад», «Рисующие руки», «Картинная галерея» и многие другие.
Например, причудливость картины «Относительность» возникает оттого, что любая поверхность нарисованного здания одновременно является и полом, и потолком, и стеной. Люди, идущие по лестницам в одном направлении, сразу спускаются и поднимаются. Здесь Эшер пытается проникнуть в суть оптической иллюзии, чем обычно занимаются ученые, а не художники. Другая известная картина "Водопад" изображает явление, невозможное в реальности - водопад как замкнутую систему, то есть питающий сам себя. Здесь Эшера занимает парадокс невозможных фигур. А в литографии «Рисующие руки» он изображает процесс самовоспроизведения, обращаясь уже к загадкам человеческого сознания. В 1958 году Эшер даже публикует теоретический труд «Последовательное деление плоскости», в котором описывает математический подход к художественному творчеству.
В ответ на отказ собратьев по кисти называть его работы искусством, Эшер окрестил искусство XX века невразумительной пачкотней, смысл которой не в силах объяснить в первую очередь те, кто ее создает. Из всех современников он ценил только Сальвадора Дали, да и то лишь за профессионализм в рисовании, а не за причудливые образы.
concepture.club
Проект по внеурочной деятельности на тему: «Математика в живописи»
Муниципальное бюджетное общеобразовательное учреждение
Аксайская Средняя Общеобразовательная школа №2
Проект
по внеурочной деятельности на тему:
«Математика в живописи»
Выполнила: ученица 5 «Е» класса
Прошкина Анна
Проверила: учитель математики
Петрова Г.С.
г. Аксай
2016
Содержание:
Введение………………………………………………………… 3
Теоретическая часть...............…………………………………. 4-13
Все состоит из фигур………………………………………. 4-6
1.1 Геометрические фигуры помогают рисовать………… 4
1.2 Мозаика, узор, орнамент………………………………. 6
Золотое сечение……………………………………………. 7
Симметрия…………………………………………………... 9
Перспектива – геометрия живописи………………………. 11
Практическая часть: рисунки, сделанные моими руками…….. 14
Заключение………………………………………………………. 15
Список используемой литературы……………………………... 16
Введение.
Математика – это царица всех наук. Её красоте, мудрости, стройности и гармонии можно только бесконечно удивляться и восхищаться. Искусство – это точное соблюдение законов математики, гармония, пропорциональность, творческое вдохновение, художественное мастерство. Законы математики действуют даже в тех областях, где их менее всего ожидалось встретить: в живописи, музыке, скульптуре. Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Мой проект «Математика в живописи» позволяет проследить взаимосвязь живописи с законами математики, которые присутствуют в окружающем мире.
Целью моей работы стал поиск взаимосвязи живописи и такой точной науки, как математика.
В ходе исследования сформировались задачи:
Изучить научно-популярную литературу и интернет источники по данной теме;
Изучить живопись различных художников, где изображены геометрические формы, алгебраические выражения;
Сделать свои рисунки с использованием математических законов.
Гипотеза: математика и живопись тесно связаны между собой.
I. Теоретическая часть.
1. Все состоит из фигур.
1.1 Геометрические фигуры помогают рисовать.
Круг, овал, квадрат, прямоугольник, треугольник. Все, что вы хотите нарисовать, можно разбить на простые фигуры. Изобразить их несложно. Прорисовывая поверх геометрических фигур желаемую картину, вы получите правильные пропорции.
ЗАДАЧА: Рассмотри картинку и разбей изображение на простые фигуры.
Если же нужно рисовать в объеме, помогут геометрические тела – цилиндр, конус, шар и другие.
Композиция картины также вписывается в ту или иную фигуру.
1.2 Мозаика, узор, орнамент.
Мозаика представляет собой кусочки материала, которыми выкладывается поверхность. Как правило, кусочки бывают разноцветными и образуют рисунок или узор. Сложность мозаики не только в выкладывании рисунка, требуется, чтобы между кусочками не оставалось зазоров, и они не перекрывали друг друга.
ЗАДАЧА: Заполнить поверхность рамки узором.
Нужно определиться с числом повторяющихся элементов узора и их размерами. Измерим длину заполняемой поверхности. В нашем случае – 10 см. Выбрали узор в виде квадрата со стороной 1 см. Тоже самое проделываем по другим сторонам рамки.
2. Золотое сечение.
В 1509 году в Италии появилась книга Луки Пачоли под названием «О божественной пропорции». В ней были установлены математические соотношения, соблюдая которые художник достигнет красоты. Иллюстрации - 60 многогранников и рисунок «Витрувианский человек » принадлежали руке Леонардо да Винчи, который известен, прежде всего, как великий
художник. Но он был разносторонним человеком, занимался математикой, физикой, химией, машиностроением, военной техникой, архитектурой. И во всех этих науках Леонардо добился успехов. Этот человек полон загадок, многие из которых до сих пор остались тайной. Его рукописи были зашифрованы, он писал так, что прочесть слова можно было только с помощью зеркала.
Леонардо да Винчи был убежден в единстве живописи и математики. Он изучал пропорцию. В его рисунке «Витрувианский человек» выражена идеальная пропорция тела человека, которая заключена в соотношении стороны квадрата и радиуса окружности. Еще одна идеальная пропорция тела была сформулирована еще во времена Древней Греции:
| Рост человека = размаху рук (от кончиков пальцев) =8 ладоням=6 ступням=8лицам |
Можно проверить эту формулу на себе.
Что же дают идеальные пропорции? Красоту! Ученые проводили опыт, предложив людям из нескольких прямоугольников выбрать один на свой вкус. Большинство остановило выбор на фигуре, в основе которой лежат идеальные пропорции, названные золотым сечением.
У золотого прямоугольника есть одно замечательное свойство. Если отсечь от него квадрат, останется тоже золотой прямоугольник. Портрет Моны Лизы, написанный Леонардо да Винчи, построен на золотом сечении, ее лицо вписано в золотые прямоугольники разного размера. В «Тайной вечере» золотые прямоугольники определяют размеры картины и положение ее персонажей.
3.Симетрия.
В математике существует несколько видов симметрии:
Центральная симметрия.
Осевая симметрия.
Зеркальная симметрия.
Но симметрия (соразмерность, одинаковость в расположении частей какого-либо рисунка относительно точки, прямой, плоскости) – это понятие не только чисто математическое. Она есть и в творениях природы (животные, листья растений, кристаллы), и в творениях конструкторов, архитекторов, скульпторов, художников.
Вернемся опять к картинам великого художника Леонардо да Винчи «Мадонна Литта». 
Обратите внимание: фигура мадонны и ребенка вписывается в правильный треугольник, который вследствие симметричности особенно ясно воспринимается глазом зрителя. Благодаря этому мать и ребенок сразу же оказываются в центре внимания, как бы выдвигаются на передний план. Голова Мадонны совершенно точно, но в то же время естественно помещается между двумя симметричными окнами на заднем плане картины. В окнах просматриваются спокойные горизонтальные линии пологих холмов и облаков. Все это создает ощущение покоя и умиротворенности, усиливаемое за счет гармоничного сочетания голубого цвета с желтоватыми и красноватыми тонами.
А теперь опять вернемся к знаменитой картине «Тайная вечеря». Двенадцать апостолов расположены вокруг своего учителя четырьмя группами: по две группы с каждой стороны от него и по три человека в каждой группе. Вся композиция строго симметрична и строго уравновешена относительно вертикальной оси, проходящей через ее главную точку.
Симметрия тесным образом связана с золотым сечением. Великий русский кристаллограф Г.В. Вульф (1863...1925) считал золотое сечение одним из проявлений симметрии.
Перспектива – геометрия живописи
“Все проблемы Перспективы можно пояснить при помощи пяти терминов Математики: точка, линия, угол, поверхность и тело”.
Леонардо да Винчи.
Слово перспектива означает насквозь видеть. Перспектива – наука, изучающая законы линейного построения изображения предметов при разном их удалении от наблюдателя. Поэтому обычно говорят о линейной перспективе. Перспективой также называют и само изображение, построенное по этим законам. Кроме линейной перспективы, существует еще так называемая воздушная перспектива.
Было разработано немало методов и приемов перспективного построения, позволяющих точно воспроизвести на плоскости любой предмет в любом повороте, на любом удалении и с любой точки зрения.
Известно, что параллельные линии на ровной местности, например рельсы и т.п., удаляясь от нас, в конце концов, зрительно сойдутся в одной точке на горизонте, т.е. на той условной линии, где сходятся земля и небо. Без линии горизонта не может обойтись ни одно перспективной построение.
Так перспективу мы можем наблюдать на таких картинах, как картина
В. Серова – «Петр I», 1907г
Клод Моне «Въезд в Ветей зимой», 1879
Виктор Васарели, 1935 « Изучение перспективы ».
Все то, что наблюдатель может охватить одним взглядом, не двигаясь и не поворачивая головы, называется полем зрения. Наиболее ясное и отчетливое восприятие предмета заключается в пределах угла, равного примерно 30 градусов. Поэтому, чтобы его воспринять отчетливо, точка зрения наблюдателя должна находиться на удалении, превышающим в 2,5-3 раза самое большое измерение этого предмета. Если же к предмету подойти ближе этого расстояния, его можно увидеть (не поворачивая головы) только частично. Если же наблюдатель будет перемещаться около предмета направо, налево, вверх, вниз, он будет представляться ему с каждой новой точки зрения по-новому, в иных поворотах и ракурсах.
Помещая на рисунке или картине людей в различном перспективном удалении, художник должен быть уверенным, что величина намеченных фигур соответствует их положению в пространстве.
Практическая часть: рисунки, сделанные моими руками.
Заключение.
Изучая тему «Математика в живописи, я пришла к выводу, что математика сыграла большую роль в развитии искусства. Отточенная красота математики прослеживается везде. Благодаря математике, наш окружающий мир совершенствуется и улучшается с каждым днем.
Мне было очень интересно изучать данную тему, так как я сама увлекаюсь изобразительным искусством и роль математики в живописи мне очень близка.
В данной работе рассмотрено только несколько законов математики, применяемых живописцами. Но этого уже достаточно, чтобы убедиться во взаимосвязи двух на первый взгляд несовместимых понятий: математика и живопись.
Такое количество материала было обработать очень сложно, но интерес к данной теме давал мне стимул для изучения. В этой теме, я не смогла охватить весь материал, и много чего ещё интересного осталось мною не изучено. Но я на этом не остановлюсь и буду изучать данную тему дальше.
Список использованной литературы.
Воротников И. Занимательное черчение. // Пособие для учащихся. / Изд. 3-е. – М.: «Просвещение», 1977. – с. 191.
Зенкевич И. Эстетика урока математики // Пособие для учителей. – М.: «Просвещение», 1981. – с. 25.
Мириманов В. XX век. Сам о себе. Персоналии и течения. Малевич // Искусство. Приложение к газете «Первое сентября». – М., 2001. – № 1. – С. 1
Мириманов В. XX век. Сам о себе. Персоналии и течения. У истоков кубизма. Искусство. Приложение к газете «Первое сентября». – М., 2001. – № 7. – С. 5-8.
Прохоров А. Золотая спираль. // Квант. Научно-популярный физико-математический журнал АН СССР и АПН СССР. – М.: «Наука», 1984. – № 9. – С. 15-17.
Самойлик Г. Леонардо да Винчи. // Математика. Приложение к газете «Первое сентября». – М., 2003. – № 4. – С. 7-10.
Чепракова Е., Липкина Т. Присутствие красоты. // Математика в школе. Научно-теоретический и методический журнал МО РФ. – М.: «Школьная пресса», 2001. – № 3. – С. 73-75.
Шарыгин И., Ерганжиева Л. Наглядная геометрия. 5-6 классы // Пособие для общеобразовательных учебных заведений. / Изд. 4-е. – М.: «Дрофа», 2001. – с. 192.
Ятайкина А., Пашкина О. О золотом сечении и не только о нем. // Математика в школе. Научно-теоретический и методический журнал МО РФ. – М.: «Школьная пресса», 2001. – № 3. – С. 75-76
12
multiurok.ru
математический Фотографии, картинки, изображения и сток-фотография без роялти
#69345533 - Science blackboard with math. Real physical equations of Einstein.. 
Вектор
Похожие изображения
Добавить в Лайкбокс
#37601189 - Abstract Background with mathematical formulas, calculations,.. Вектор
Похожие изображения
Добавить в Лайкбокс
#50883152 - Complex math formulas on whiteboard. Mathematics and science..
Похожие изображения
Добавить в Лайкбокс
#35401743 - Mathematical vector seamless pattern with figures and calculations... Вектор
Похожие изображения
Добавить в Лайкбокс
#41677252 - Mathematical formulary imprints on white Sphere.
Похожие изображения
Добавить в Лайкбокс
#38268813 - Mathematics equations and formulas on a white background
Похожие изображения
Добавить в Лайкбокс
#50745252 - Math theory and mathematical formula equation doodle handwriting.. Вектор
Похожие изображения
Добавить в Лайкбокс
#49180481 - Statistic math law theory and mathematical formula equation doodle.. Вектор
Похожие изображения
Добавить в Лайкбокс
#52997665 - Businessman sitting on a chair and studying math formulas on..
Похожие изображения
Добавить в Лайкбокс
#34215720 - A young teacher concentrated reading a book
Похожие изображения
Добавить в Лайкбокс
#43504300 - Hand Drawn Scribble Infinity sign. emblem endless. The concept.. Вектор
Похожие изображения
Добавить в Лайкбокс
#30596506 - Math, mathematics symbol Calculation, calculator concept Plus,.. Вектор
Похожие изображения
Добавить в Лайкбокс
#56408721 - basic colorful mathematical symbols equal less greater Вектор
Похожие изображения
Добавить в Лайкбокс
ru.123rf.com
Презентация по математике "Математика в изобразительном искусстве"
Презентация на тему: Математика в изобразительном искусствеСкачать эту презентацию
Скачать эту презентацию
№ слайда 1
Описание слайда: « Математика в изобразительном искусстве»Исследовательская работа по математике ученицы 10 класса «А» средней школы № 19 Галита Анастасии Преподаватель: Воеводина О.А
№ слайда 2
Описание слайда: Исторически, математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы, подразумевающем реалистичное изображение трехмерной сцены на плоском холсте или листе бумаги. Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная. Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания. Несколько значительных фигур в изобразительном искусстве проложили дорогу этим индивидуумам.
№ слайда 3
Описание слайда: Голландский художник М.К. Эшер (1898-1972) в некотором роде является отцом математического искусства. Математические идеи играют центральную роль в большинстве его картин за исключением лишь ранних работ. Большинство идей, часто используемых современными математическими художниками, были использованы Эшером, и его работы часто являются источником вдохновения для современных авторов.
№ слайда 4
Описание слайда: Темы наиболее часто использующиеся в изобразительном искусствеМногогранникЛента МебиусаНевозможные фигурыТесселяцияФракталыИскаженные перспективы
№ слайда 5
Описание слайда: Многогранники Многогранник - это трехмерное тело, гранями которого являются многоугольники. Существует всего пять правильных многогранников, у которых все стороны являются правильными многоугольниками и все вершины одинаковы. Они известны как многоугольники Платона или Платоновы тела. Также существует 13 выпуклых многогранников, гранями которых являются один, два или три правильных многоугольника, и у которых все вершины одинаковы. Они известны как тела Архимеда. Кроме этого существует бесконечное множество призм и антипризм с гранями в виде правильных многоугольников. Эшер использовал многогранники во многих своих работах, включая "Рептилии" (1949), "Двойной планетоид" (1949) и "Гравитация" (1952).
№ слайда 6
Описание слайда: Тесселляции Тесселляции, известные также как покрытие плоскости плитками, являются коллекциями фигур, которые покрывают всю математическую плоскость, совмещаясь друг с другом без наложений и пробелов. Правильные тесселляции состоят из фигур в виде правильных многоугольников, при совмещении которых все углы имеют одинаковую форму. Существует всего три многоугольника, пригодные для использования в правильных тесселляциях. Это - правильный треугольник, квадрат и правильный шестиугольник. Полуправильными тесселляциями называют такие тесселляции, в которых использованы правильные многоугольники двух или трех типов и все вершины одинаковы. Существует всего 8 полуправильных тесселляций. Вместе три правильных тесселляции и восемь полуправильных носят название Архимедовых. Тесселляции, в которых отдельные плитки являются узнаваемыми фигурами, являются одной из основных тем творчества Эшера. В его записных книгах содержатся более 130 вариантов тесселляций.Он использовал их в огромном количестве своих картин, среди которых "День и ночь" (1938), серия картин "Предел круга" I-IV, и знаменитые "Метаморфозы" I-III (1937-1968). Примеры ниже - картины современных авторов Холлистера Девида и Роберта Фатауэра.
№ слайда 7
Описание слайда: HOLLISTER DAVID "СЕМЬ ПТИЦ". НА ЭТОЙ КАРТИНЕ ИЗОБРАЖЕНЫ СЕМЬ ПТИЦ, ДВЕ ИЗ КОТОРЫХ ИЗОБРАЖЕНЫ В НЕГАТИВЕ НА ФОНЕ ЛАНДШАФТА ГОРОДА АХО В АРИЗОНЕ. ПОСЛЕДОВАТЕЛЬНО УМЕНЬШАЮЩИЕСЯ ФИГУРЫ ПТИЦ СОВМЕЩАЮТСЯ ДРУГ С ДРУГОМ В ВИДЕ ФРАКТАЛЬНОЙ ТЕССЕЛЛЯЦИИ. ХВОСТОВЫЕ ПЕРЬЯ КАЖДОЙ ПТИЦЫ ЯВЛЯЮТСЯ РАЗДЕЛЯЮТ КОНСТРУКЦИЮ НАПОПОЛАМ, ОТСЕКАЯ ПРИМЕРНО ТРЕТЬ РАССТОЯНИЯ МЕЖДУ КОНЧИКАМИ КРЫЛЬЕВ. КАЖДАЯ МЕНЬШАЯ ПТИЦА В СВОЮ ОЧЕРЕДЬ ДЕЛИТ СВОЮ ОБЛАСТЬ АНАЛОГИЧНЫМ ОБРАЗОМ. ЕСЛИ ЭТОТ ПРОЦЕСС ПРОДОЛЖАТЬ ДО БЕСКОНЕЧНОСТИ, ПОЛУЧИТСЯ НАБОР ТОЧЕК, ИЗВЕСТНЫЙ КАК МНОЖЕСТВО КАНТОРА ИЛИ КАНТОРОВА ПЫЛЬ.
№ слайда 8
Описание слайда: Robert Fathauer "Фрактальные рыбы - сгруппированные группы". Это компьютерная работа, распечатанная на фотобумаге. Сквозь иллюминатор видны волны, но при ближайшем рассмотрении видно, что волны являются на самом деле фрактальной тесселляцией, состоящей из рыб.
№ слайда 9
Описание слайда: Искаженные и необычные перспективы Необычные системы перспективы, содержащие две или три исчезающие точки, также являются излюбленной темой многих художников. К ним также относится родственная область - анаморфное искусство. Dick Termes "Клетка для человека" (1978)
№ слайда 10
Описание слайда: Невозможные фигуры Невозможные фигуры - эти фигура, изображенная в перспективе таким способом, чтобы выглядеть на первый взгляд обычной фигурой. Однако при более внимательном рассмотрении зритель понимает, что такая фигура не может существовать в трехмерном пространстве. Эшер изобразил невозможные фигуры на своих известных картинах "Бельведер" (1958), "Восхождение и спуск" (1960) и "Водопад" (1961). Одним из примеров невозможной фигуры служит картина современного венгерского художника Иштвана Ороса
№ слайда 11
Описание слайда: Лента Мебиуса Лента Мебиуса - это трехмерный объект, имеющий только одну сторону. Такая лента может быть легко получена из полоски бумаги, перекрутив один концов полоски, а затем склеив оба конца друг с другом. Эшер изобразил ленту Мебиуса на работах "Всадники" (1946), "Лента Мебиуса II (Красные муравьи)" (1963) и "Узлы" (1965).
№ слайда 12
Описание слайда: Фракталы Фрактал - это объект, повторяющий сам себя в различных масштабах, которые связаны математическим способом. Фракталы формируются итерационно, многократно повторяя вычисления так, что получается объект высокой сложности с множеством мелких деталей. К сожалению, фракталы как таковые были недоступны Эшеру, потому что были формализованы и выделены в отдельную область математики лишь после его смерти. Эшер очень интересовался изображением бесконечного в пределах конечной области, в частности бесконечными тесселляциями. Он использовал сжимающиеся координатные сетки и гиперболическую геометрию для достижения этого эффекта, как показано в картинах "Предел круга" I-IV (1958-1960) и "Предел квадрата" (1964). Ниже приведены примеры современных художников Кэри Митчелл и Роберта Фатауэра.
№ слайда 13
Описание слайда: Kerry Mitchell "Будда" - компьютерная картина основанная на множестве Мандельброта, исследованного Бенуа Мандельбротом
№ слайда 14
Описание слайда: Robert Fathauer "Композиция кругов" (2001) - не является вычисляемым фракталом, однако может быть получен графически, упаковывая меньшие круги в больших.
№ слайда 15
Описание слайда: Связь математики и изобразительного искусства при конструктивном построении натюрморта. Натюрморт (фр. nature morte — букв. «мертвая природа») — изображение неодушевлённых предметов в изобразительном искусстве, в отличие от портретной, жанровой, исторической и пейзажной тематики.При построении натюрморта используются такие понятия как: параллельные прямые, геометрические фигуры, отношения, пропорции, оси симметрии. Приведём пример построения на простейшем натюрморте, состоящем из трёх предметов(ваза, кружка, груша)
№ слайда 16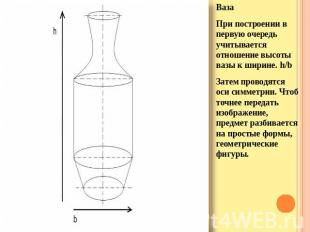
Описание слайда: ВазаПри построении в первую очередь учитывается отношение высоты вазы к ширине. h/bЗатем проводятся оси симметрии. Чтоб точнее передать изображение, предмет разбивается на простые формы, геометрические фигуры.
№ слайда 17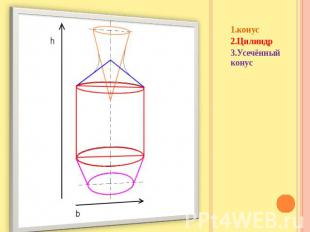
Описание слайда: 1.конус 2.Цилиндр3.Усечённый конус
№ слайда 18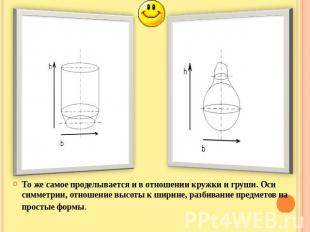
Описание слайда: То же самое проделывается и в отношении кружки и груши. Оси симметрии, отношение высоты к ширине, разбивание предметов на простые формы.
№ слайда 19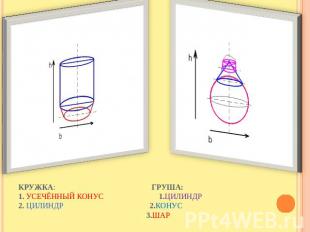
Описание слайда: Кружка: Груша:1. Усечённый конус 1.Цилиндр2. Цилиндр 2.Конус 3.Шар
№ слайда 20
Описание слайда: Соединяем три элемента . При этом мы должны учитыватьотношение размеров предметов относительно друг друга, т. е. сколько раз высота груши помещается в высоту вазы, ширина кружки в высоту груши и т. д. При построении овалов учитывается перспектива, чем ниже овал относительно уровня глаз, тем больше он раскрыт. Все оси овалов в каждом предмете строго параллельны друг другу. Кружка и ваза строго симметричны относительно осей симметрии.
№ слайда 21
Описание слайда: МНОГИЕ ХУДОЖНИКИ В СВОИХ РАБОТАХ ИСПОЛЬЗУЮТ МАТЕМАТИКУ. НАДЕЮСЬ, ЧТО В СВОЕЙ РАБОТЕ Я ДОКАЗАЛА, ЧТО, КАЗАЛОСЬ БЫ, ТАКИЕ ОТДАЛЁННЫЕ ДИСЦИПЛИНЫ КАК МАТЕМАТИКА И ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО ПЕРЕСЕКАЮТСЯ ДРУГ С ДРУГОМ, А В ТВОРЧЕСТВЕ НЕКОТОРЫХ ХУДОЖНИКОВ ОНИ ОЧЕНЬ ТЕСНО СВЯЗАНЫ.
ppt4web.ru
Математика в картинках
Разделы: Математика
Математика – наука весьма сложная для учащихся, поэтому нельзя упускать ни одного подхода, делающего её более доступной; подхода, позволяющего связать излагаемый материал с имеющимися у школьника знаниями и образами.
Эффективность преподавания математики, как и любого другого предмета в школе, зависит от многих факторов, одним из которых является наглядность.
Наглядность – это мощное воздействующее средство на восприятие ребёнка при обучении. Наглядность, используемая в учебниках, настенных таблицах, печатных типовых плакатах, редких диафильмах не производит на современных школьников нужного впечатления, не помогает изучению. Все знают, что большую часть информации дети получают с экрана телевизора и из компьютера, таким образом, у них развивается зрительное восприятие материала.
Английский математик Годфри Гарольд Харди говорил о творческом подходе к математике: “Творчество математика в такой же степени есть создание прекрасного, как творчество живописца или поэта, – совокупность идей, подобно совокупности красок или слов, должно обладать внутренней гармонией. Красота есть первый пробный камень для математической идеи, в мире нет места уродливой математике”.
Математикам
очень часто помогает … цвет. Вот, например, одно
из “цетных” доказательств теоремы Пифагора. На
рисунке красным цветом выделен центральный
прямоугольный треугольник, а красной штриховкой
– еще шесть ему равных. Теперь нетрудно увидеть,
что сумма площадей двух жёлтых квадратов равна
площади зелёного квадрата. Доказана теорема
Пифагора!
В математике существует много задач и теорем о различных раскрасках. Наиболее знаменитая из них – проблема четырёх красок, которой “переболели” тысячи любителей и математиков.
Ориентируясь на эти особенности, а так же на своё стремление развивать в детях творческое мышление и активизировать их познавательную деятельность, я создала “учебные математические картины”.
Во-первых, красочность и необычность привлекает любого ребёнка. Во-вторых, название каждой картины заставляет задуматься над связью с изучаемым материалом. В-третьих, картины можно применять на уроках при объяснении нового материала, в процессе изучения темы, при повторении и в виде заданий поискового характера. Они содержат в себе теоретические моменты, простые и трудные задачи. В-четвёртых, картины содержат дополнительный материал, который не входит в школьный курс математики. В-пятых, они поддерживают и укрепляют межпредметные связи (алгебра –геометрия – физика ).
Сами оригиналы “учебных картин” (размером 30х40см) находятся в кабинете, где я преподаю. Это – украшение и своеобразное напоминание учащимся об изучаемом материале, призыв: “Вспоминай, думай, рассуждай!”
Давайте познакомимся с “учебными картинами” поближе. Картина №1 называется “Точка – царица геометрии”. Когда демонстрируешь её с дальнего расстояния, то чётко просматриваются круги и квадраты разных размеров. Если подойти поближе, видишь, что фон и сами фигуры состоят из точек. Сколько здесь точек?..Попробуйте в квадрате 10х10 см поставить 100, 1000, 10000 точек. Дети воспринимают игру с удовольствием, но потом быстро устают. Не в этом суть! Мы уже добились внимания учащихся , а это самое главное на уроке.
Каждый может представить себе каплю дождя, каплю воды из крана, каплю росы. Чтобы представить “Графическую каплю” надо посмотреть на следующую картину. Эта капля приковывает внимание зрителя своим красочным многообразием, возможностью пофантазировать, как Н.В.Лобачевский, исследуя поверхность, увидеть обычные графики в необычных условиях.
Многие учителя математики при произнесении словосочетаний описанная окружность или описанные многоугольники ловят улыбку на лицах своих учеников. Советую перед введением данных понятий обратить внимание на картину “Четырёхугольная кругообразность”. Когда учащиеся увидят своими глазами то, о чём пойдёт речь, им возможно будет легче сосредоточиться на понимании содержания материала.
Может ли быть пустая консервная банка объединить физику с геометрией? Что за таинственный узор её покрывает? Какой отрезок длиннее? На эти и многие другие вопросы по теме “Вектор” помогает ответить картина “Цилиндрическое направление”.
“Бесподобное подобие” медленно по спирали домика улитки втягивает ребят в лабиринт из задач по теме “Подобие”. Радужные полосы напоминают детскую рифмовку из физики: “Каждый охотник желает знать, где сидит фазан”. Прямоугольные треугольники с катетами по 1см не только скрывают иррациональное число v2, но и являются условиями для других геометрических задач.
Красивое название “Пробуждение эпитрохоиды” – не игра слов, а упражнения по составлению уравнений окружности и повод для размышления любознательным.
“Единство функциональной зависимости” – задание для учащихся 10 – 11-х классов, которые с большим интересом вниманием будут всматриваться в переплетение тел дракона и змеи, тем самым изучая колебания синусоиды и косинусоиды.
Все эти учебные пособия успешно применяются мной на уроках. Они вносят свежее дуновение фантазии и разнообразия в строгие ряды цифр и знаков.
Примерные задания по “учебным картинам” и варианты их использования.
№1. “Точка – царица геометрии”
Используется для вводной беседы по геометрическому материалу в 5 классе (“Точка. Прямая линия”) и в 7 классе (“Начальные геометрические сведения”).
№2. “Графическая капля”
Используется при изучении темы “Графики функций” в 9 классе.
Задание:
- Найдите графики функций, изображенных на картине и запишите им соответствующие формулы.
Ответ:
у = х2; у = – 3; у = х2; у = х; х2 + у2 = 4; у = – 6/х; (х – 3)2 + (у – 4)2 = 1.
№3. “Четырёхугольная кругообразность”
Используется для изучения темпо геометрии в 8 классе “Четырехугольники” и “Вписчанные и описанные четырёхугольники”.
Задания:
- Какие четырёхугольники изображены на картине? Перечислите их, дайте определение каждому, расскажите какими свойствами и признаками они обладают. (Квадрат, параллелограмм, прямоугольник, ромб, прямоугольная трапеция, равнобедренная трапеция).
- Что вы знаете о вписанных многоугольниках? Около любого четырёхугольника можно описать окружность? Около каких четырёхугольников на картине описаны окружности? (Прямоугольник, квадрат).
- Какие многоугольники называются описанными около окружности? В какие четырёхугольники можно вписать окружность? Какие описанные четырёхугольники изображены на картине? (Ромб, квадрат).
№4. “Цилиндрическое направление”
Используется в 8-ом и 9-ом классах для изучения темы “Вектор”.
Задания:
- Покажите на картине равные векторы; сонаправленные векторы, но не равные.
- Покажите противоположные векторы; протиположно направленные, но не противоположные.
- Являются ли “желтые” векторы коллинеарными?
- Дайте определение коллинеарным векторам.
- Покажите вектор коллинеарный “зелёному” и т.д.
- Являются ли “коричневый” и “красный” векторы – равными? и т.п.
№5. “Бесподобное подобие”
Используется на уроках геометрии в 8 классе при изучении темы “Подобные треугольники”.
Задания:
- Что вы можете рассказать о методе подобия?
- Приведите примеры подобных фигуг испоьзуя изображение на картине.
- Подобны ли изображенные на картине прямоугольные треугольники с катетом 1см?
- Сколько сантиметров в гипотенузе самого большого “красного” равнобедренного треугольника, если катеты самого матенького “чёрного” равны 1см?
- Что напоминает окрас улитки? Какие вы знаете “подсказки” , чтобы запомнить цвета радуги?
- Что такое спектр? Что вы знаете про белый и чёрный чвета? (Рассматриваерся дополнительно на основе уроков физики).
- Что общего между нашей улиткой и у л и т к о й П а с к а л я? (Дополнительное задание исследовательского характера ).
№6. “Пробуждение эпитрохоиды”
Используется на уроках в 9 классе при изучении темы “Уравнение окружности”.
Задания:
- Напишите уравнения девяти изображенных на картине окружностей.
Ответ:
(х – 1 )2 + (у – 7)2 = 0,25; (х – 5)2 + (у – 6)2 = 0,25; (х – 3)2 + (у – 5)2 = 0,25; (х + 1,5)2 + (у – 4)2 = 1; (х – 2)2 + (у – 2)2 = 4; (х – 5)2 + у2 = 1; х2 + (у + 1)2 = 1; (х – 2,5)2 + (у + 1)2 = 16; (х – 4)2 + (у + 2,5)2 = 4.
- Кто поможет “распуститься” т р о х и о д а л ь н о й розе? (Дополнительное задание исследовательского характера.)
№7. “Единство функциональной зависимости”
Используется в 9–11 классах при изучении тригонометрических функций.
Задание:
- Напишите все семь формул, задающих указанные на картине функции.
Ответ:
у = соs x; у = 2соs х/2; у = sin х; у = 1/2sin х; у = 1/2sin 2х – 1,5; у = 2 соs x; у = 3sin 2х.
xn--i1abbnckbmcl9fb.xn--p1ai
Фоменко картины, творческое наследие СССР, Графика Анатолия Фоменко
Анатолий Фоменко приобрел более-менее широкую известность, как автор «Новой хронологии» — труда, предполагающего существенное переосмысление традиционной истории и признанного антинаучным. Углубляться в дебри методологии, предложенной Анатолием Тимофеевичем для определения датировки исторических событий мы не будем, хоть это вне всяких сомнений достаточно интересная тема, пересекающаяся, к тому же, во многих аспектах с абсолютно недостоверной и, порой даже фантастической информацией от «представителей элитной династии» и прочих граждан, претендующих на звание «истинно сильных мира сего».
Но для нас Анатолий Тимофеевич интересен не как историк и даже вне контекста его основной научной деятельности, не вызывающей ни у кого сомнений в своей научности. Тут можно вспомнить расхожее мнение, что талантливый человек — талантлив во всем и поведать, что Фоменко, которому 13 марта сего года исполнилось 70 лет, за свою достаточно долгую жизнь добился весомых успехов в изучении математики, а точнее — различных направлений геометрии, названия которых ничего подавляющему большинству обывателей не скажут.
На поприще математических наук Анатолий Тимофеевич и добился своих основных, признанных практически всеми, успехов — он профессор, доктор математических наук, научный руководитель многих выдающихся современных ученых, автор целой уймы тематических публикаций, начиная от статей, заканчивая учебниками и крупными монографиями, действительный член РАН, РАЕН и т. д. и т. п.
Анатолий Тимофеевич успел испробовать свои силы и на литературном поле — в конце 50-х, в журнале «Пионерская правда» был опубликован его фантастический рассказ «Тайна Млечного пути». Фоменко в то время был выпускником школы. А более зрелом возрасте он работал заместителем главреда журнала «Вестник МГУ». Но и не литератор Фоменко нам интересен.
Представить вам мы хотели бы Анатолия Фоменко — выдающегося художника, создающего по истине удивительные графические картины. Эта грань его личности, к великому нашему удивлению, была бессовестно забыта и практически игнорируется, несмотря на то, что художественный стиль Фоменко — удивителен и математичен. В свое время советская публика, по всей видимости, просто не сумела воспринять работы Анатолия Тимофеевича, уж больно они сюрреалистичны и никак не вписываются в квадратно-прямоугольные рамки мышления подавляющего большинства граждан того времени. Ни серпа с молотом, ни портретов вождей, ни воодушевляющих слоганов — ничего близкого сердцу советского человека. Каракули какие-то.
Футуризм, сюрреализм, символизм, научность, экспрессивность — перечислять подходящие эпитеты, чтобы описать графические работы Анатолия Фоменко можно было бы долго, но лучше, как говорится, один раз увидеть.
Так увидьте же!
estetico.me
