Музей ЧерномырдинаЗаписки недизайнера. Картины золотое сечение
золотое сечение | Рисуем вместе
«Золотое сечение» уже давно стало синонимом слова «гармония». Словосочетание «золотое сечение» обладает просто магическим действием. Если вы выполняете какой-то художественный заказ (неважно, картина это, скульптура или дизайн), фраза «работа сделана в полном соответствии с правилами золотого сечения» может стать прекрасным аргументом в вашу пользу – проверить заказчик скорее всего не сможет, а звучит это солидно и убедительно. При этом немногие понимают, что же скрывается под этими словами. Между тем, разобраться, в том, что такое золотое сечение и как оно работает, достаточно просто.
Золотое сечение – это такое деление отрезка на 2 пропорциональные части, при котором целое так относится к большей части, как большая к меньшей. Математически эта формула выглядит так: с : b = b : а или a : b = b : c.
Итогом алгебраического решения данной пропорции будет иррациональное число Ф (Ф в честь древнегреческого скульптора Фидия).
Я не буду приводить само уравнение, чтобы не загружать текст. При желании, его можно легко найти в сети. Скажу только, что Ф будет приблизительно равным 1,618. Запомните эту цифру, это числовое выражение золотого сечения.
Итак, золотое сечение – это правило пропорции, оно показывает соотношение частей и целого.
На любом отрезке можно найти «золотую точку» — точку, которая делит этот отрезок на части, воспринимаемые как гармоничные. Соответственно, так же можно разделить любой объект. Для примера построим прямоугольник, поделенный в соответствии с «золотой» пропорцией:
Отношение большей стороны получившегося прямоугольника к меньшей будет приблизительно равно 1,6 (заметьте, меньший прямоугольник, получившийся в результате построений, также будет золотым).
Вообще, в статьях, объясняющих принцип золотого сечения, встречается множество подобных рисунков. Объясняется это просто: дело в том, что найти «золотую точку» путем обычного измерения проблематично, поскольку число Ф, как мы помним, иррациональное. Зато, такие задачи легко решаются геометрическими методами, с помощью циркуля и линейки.
Однако, наличие циркуля для применения закона на практике совсем не обязательно. Есть ряд чисел, которые принято считать арифметическим выражением золотого сечения. Это ряд Фибоначчи. Вот этот ряд:
0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.
Запоминать эту последовательность не обязательно, ее можно легко вычислить: каждое число в ряду Фибоначчи равно сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.
Один из самых древних (и не потерявших свою привлекательность до сих пор) символов, пентаграмма – прекрасная иллюстрация принципа золотого сечения.
В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны). (цитата из Википедии).
Почему же «золотая пропорция» представляется такой гармоничной?
У теории золотого сечения есть масса как сторонников, так и противников. Вообще, идея о том, что красоту можно измерить и просчитать с помощью математической формулы, симпатична далеко не всем. И, возможно, эта концепция действительно казалась бы надуманной математической эстетикой, если бы не многочисленные примеры природного формообразования, соответствующие золотому сечению.
Сам термин «золотое сечение» ввел Леонардо да Винчи. Будучи математиком, да Винчи также искал гармоничное соотношение для пропорций человеческого тела.
“Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.
Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
Постепенно, золотое сечение превратилось в академический канон, и когда в искусстве назрел бунт против академизма, про золотое сечение на время забыли. Однако, в середине XIX века эта концепция вновь стала популярной благодаря трудам немецкого исследователя Цейзинга. Он проделал множество измерений (около 2000 человек), и сделал вывод, что золотое сечение выражает средний статистический закон. Помимо людей, Цейзинг исследовал архитектурные сооружения, вазы, растительный и животный мир, стихотворные размеры и музыкальные ритмы. Согласно его теории, золотое сечение является абсолютом, универсальным правилом для любых явлений природы и искусства.
Принцип золотой пропорции применяется в разных сферах, не только в искусстве, но и в науке и в технике. Будучи настолько универсальной, она, конечно, подвергается множеству сомнений. Часто проявления золотого сечения объявляются результатом ошибочных вычислений или простого совпадения, (а то и подтасовки). В любом случае, к любым замечаниям, как сторонников теории, так и противников, стоит относиться критически.
А о том, как этот принцип применять на практике, можно прочитать здесь.
Вернуться на главную страницу
Еще почитать:
artfound.ru
Золотое сечение как способ понимания настоящего искусства
Золотое сечение – это математическая формула, результат сложных расчётов, сделанных ещё древнегреческими учёными. Уникальность и божественная природа золотого сечения объясняется тем, что его использование привносит в науку, музыку, архитектуру и даже природу невидимый, но подсознательно уловимый порядок.
Золотое сечение – это такое пропорциональное гармоническое деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей. Это высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и даже в природе.
Прорции золотого сечения выглядят так
Считается, что понятие «золотого сечения» открыл древнегреческий философ и математик Пифагор. Хотя, существует мнение, что он доработал исследование более древних учёных – вавилонян или египтян. Об этом свидетельствуют идеальные пропорции пирамиды Хеопса и многие сохранившихся египетских храмов соответствуют золотому сечению.
Особое внимание на правило золотого сечения обратили художники эпохи Возрождения, обращаясь к наследию древних греков. Само понятие этой гармонической пропорции - «золотое сечение» - принадлежит Леонардо да Винчи. В его работах его использование достаточно очевидно.
К примеру, известная всем работа «Тайная вечеря» - пример использования золотого сечения.
Золотое сечение. "Тайная вечеря" да Винчи
По мнению французского архитектора ХІХ века Виолле-ле-Дюка, форма, которую невозможно объяснить, никогда не будет красивой.
Вертикальное золотое сечение можно увидеть и на картине "Троица" Андрея Рублёва.
Золотое сечение. Рублёв "Троица"
Повторяя равные величины, чередуя равные и неравные величины в пропорциях золотого сечения, художники создают на картинах тот или иной ритм, вызывают у зрителя то или иное настроение и вовлекая его в рассматривание изображения. В такие моменты человек, даже не искушённый в искусстве, подсознательно понимает, что картина ему чем-то нравится, что на неё приятно смотреть.
Пересечения линий золотого сечения образуют на плоскости четыре точки, так называемые зрительные центры, которые расположены на расстоянии 3/8 и 5/8 от краёв картины. Именно на этих точках выгоднее всего размещать ключевые фигуры картины. Это связано с тем, как устроен человеческий глаз, как работает мозг и наше восприятие.
Например, на картине Александра Иванова «Явление Христа народу» линии золотого сеченияпересекаются чётко на фигуре Христа вдали. И хотя фигуры на переднем плане значительно больше по размерам и выписаны чётче, взгляд притягивает именно размытая фигура Христа, потому что она размещена в зрительном центре.
Золотое сечение. Александр Иванов. «Явление Христа народу»
Художник Николай Крымов писал: «Говорят: искусство не наука, не математика, что это творчество, настроение и что в искусстве ничего нельзя объяснить – глядите и любуйтесь. По-моему, это не так. Искусство объяснимо и очень логично, о нём можно и нужно знать, оно математично… Можно точно доказать, почему картина хороша и почему плоха».
В изобразительном искусстве чаще используется упрощённое правило золотого сечения – так называемое «правило третей», когда картина условно делится на три равные части по вертикали и по горизонтали, образуя четыре ключевые точки.
Русский художник Василий Суриков в своей монументальной работе «Боярыня Морозова» использовал одну из этих четырёх точек, разместив в верхней левой части картины голову и правую руку главной героини полотна. Таким образом, все точки, равно как и все линии и взгляды на картине обращены к той точке.
Теперь попробуйте сами определить точки золотого сечения на следующих картинах.
Работа Константина Васильева «У окна» достаточно проста для этого задания. Линии золотого сечения в ней сходятся точно на лице героини, на её глазах, что заставляет зрителя окунуться в размышления о её переживаниях.
Золотое сечение. Константин Васильев. «У окна»
Или ещё один пример акцентирования нашего внимания – картина «Луиза Сан-Феличе в заточении» Джоваччино Тома. Опять же, нетрудно заметить, что и здесь линии золотого сеченияпересекаются на лице героини.
Золотое сечение. Джоваччино Тома. «Луиза Сан-Феличе в заточении»
Теперь вы, наверняка, будете пытаться распознать божественную гармонию золотого сечения на каждой увиденной картине.
worldartdalia.blogspot.com
Основные построения золотого сечения - Записки недизайнера
На практике при выборе формата листа (картины) часто используют «классические» пропорции сторон прямоугольника, в котором отношение меньшей стороны к большей составляет число 0,6180339, а большей к меньшей — 1,6180339. Эти числа с древнейших времён называют золотыми, а отношение величин, необходимое для их получения, известно как золотая пропорция или золотое сечение.Основа учения о гармонии мира, выраженная в числовых отношениях, была заложена древнегреческим учёным-математиком Пифагором (VI в до н.э). Им представлено золотое сечение как одна из закономерностей, математически точно определяющая наиболее красивое и гармоничное соотношение частей целого, разделённого на две неравные половины.
На соотношении частей отрезка в пропорциях золотого сечения основано построение прямоугольника. С помощью диагоналей осуществляется членение его на составные части, при котором образуется динамика пропорциональных фигур — квадрата, прямоугольника, а также прямоугольного и равнобедренного треугольников.
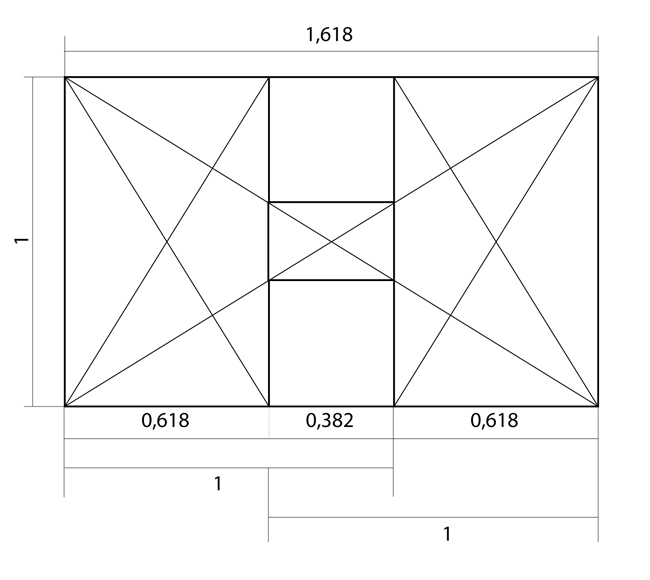Т.о., используя диагонали можно получить последовательный ряд увеличивающихся прямоугольников, с соотношением сторон — 1:√ 2, 1:√3, 1:√4, 1:√5, производных от квадрата.
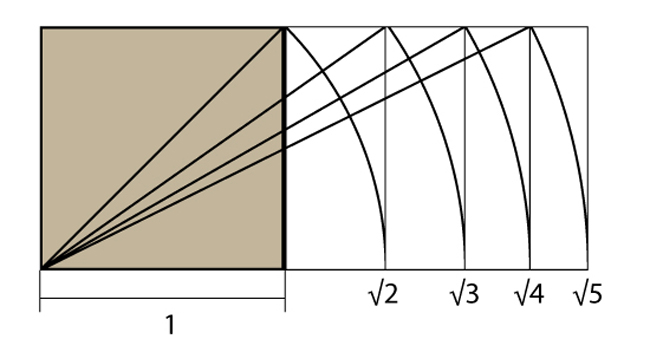При стороне √4 образуется прямоугольник с удвоенным квадратом. При стороне √3 образуется два прямоугольных треугольника, у которых общая гипотенуза является диагональю прямоугольника, равная удвоенной величине меньшего катета (т.е. стороне квадрата), и они имеют острые углы 30 и 60 градусов.
Диагональ используется и в построении последовательно увеличивающихся квадратов, создающих «динамическое» развитие их величины.
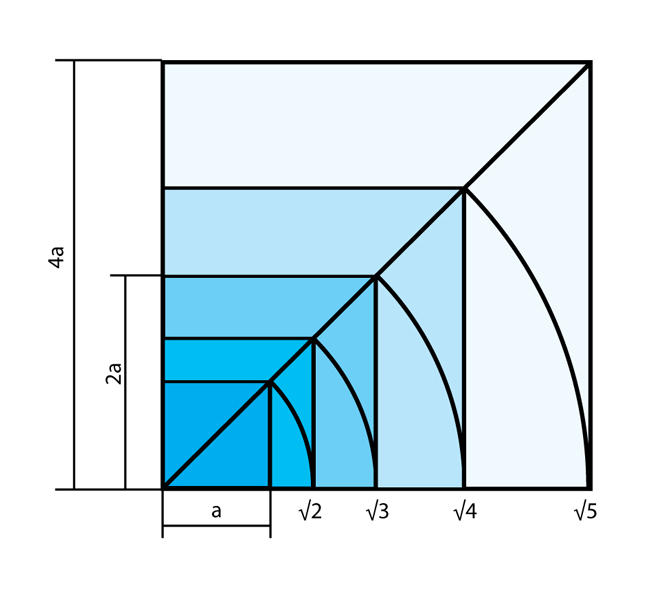В этом построении сторона каждого последующего квадрата относится к стороне предыдущего, как диагональ квадрата к его же стороне. Эти преобразования иногда называют «активным квадратом».
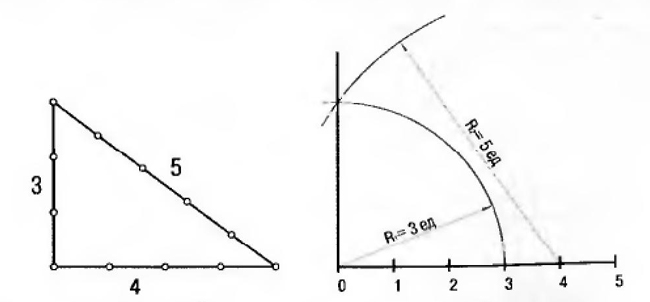
Геометрическая система динамических пропорций квадрата, прямоугольника и треугольника были основой в создании архитектурных сооружений в ранний период Древнего Египта. Кроме того, в условиях примитивной техники архитектурного строительства в те далёкие времена постоянно требовалось восстановление перпендикуляра к прямой, которое осуществлялось тогда при помощи верёвки с 12 узлами. С использованием такого приспособления получался прямоугольный треугольник с отношением строно - 3:4:5, который впоследствии стали называть египетским. В настоящее время на его основе строят прямые углы и проводят перпендикуляры к концу отрезка.
С древнейших времён золотое сечение используется в практике построения различных изображений. Это способствует созданию гармоничных образов и уравновешенности пропорций во всём, что на окружает. Пропорции золотого сечения присутствуют в мамематике, и особенно в геометрии, в изобразительном искусстве, в быту и в природе, в растительном и животном мире.
Золотое сечение получило широкое развитие в математике. Так, в XVI веке итальянский учёный Фибоначчи выстроил математический ряд цифр, при котором последующее число определяет сумму двух предыдущих - 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. Кроме того, устанавливается и другая зависимость этих чисел, при которой отношение каждого последующего к предыдущему выражается числом 1,618..., а предыдущего к последующему - 0,618. Таким образом, в этом математическом ряду образуется взаимосвязь чисел, содержащая пропорции золотого сечения.
Особенно часто золотое сечение используется в геометрии при делении окружности на равные части и построении правильных многоугольников.
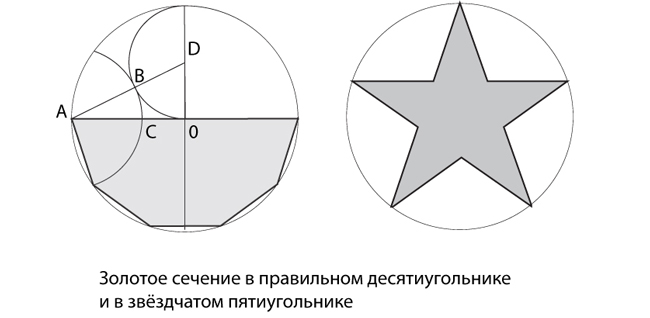
В звёздчатом многоугольнике - пятиконечной звезде, каждая точка пересечения её сторон делит их на две неравные части в пропорциях золотого сечения.
С древнейших времён золотое сечение применялось в различных видах изобразительного искусства - в архитектуре, вкульптуре, живописи. Парфенон - классический пример применения золотого сечения в архитектуре.
Особенно широко использовал в своём творчестве соотношение величин золотого сечения Леонардо да Винчи, которое он назвал «божественная пропорция».
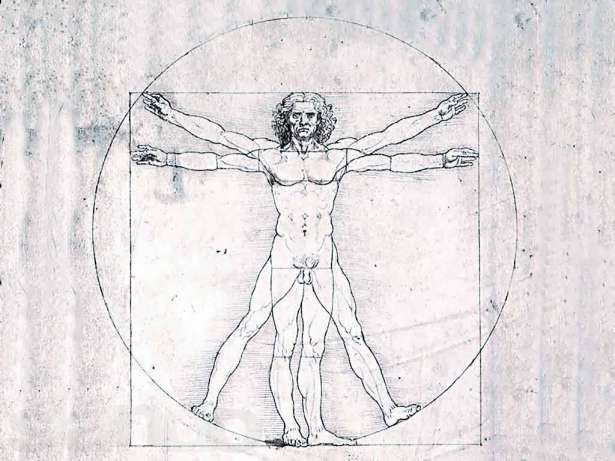
Числовой гармонии золотого сечения подчиняются также античные статуи греческого искусства, отражающие пропорции идеально сложённого человеческого тела.
Золотое сечение применяют в начертании букв и цифр различного шрифта.
Золотое сечение часто используют в определении величины прямоугольника при заданной его большей или меньшей стороне. Если у прямоугольной картины задана длина (АВ), то её высоту (АС) определяют следующим построением:
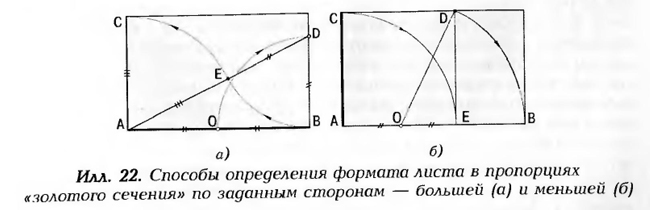Сначала из конца отрезка (В) проводят дугу, равную его половине до пересечения с перпендикуляром (АО=ОВ=ВД). Полученную точку Д соединяют прямой с другим концом отрезка (А). Затем из точки Д проводят дугу радиусом ВД до пересечения с этой прямой и отмечают точку Е. Дуга, проведённая из конца отрезка А радиусом АЕ определяет по вертикальной прямой точку С и искомую высоту картины АС.
Если задана высота картины (АС), то её длину (АВ) определяют другим построением. Сначала строят квадрат АСДЕ со стороной равной АС. Затем из середины стороны квадрата (О) проводят дугу радиусом ОД и получают на горизонтальной прямой точку В, которая определит искомую длину стороны прямоугольной картины АВ.
По прямоугольнику с золотыми пропорциями можно построить любой величинны подобный формат листа.
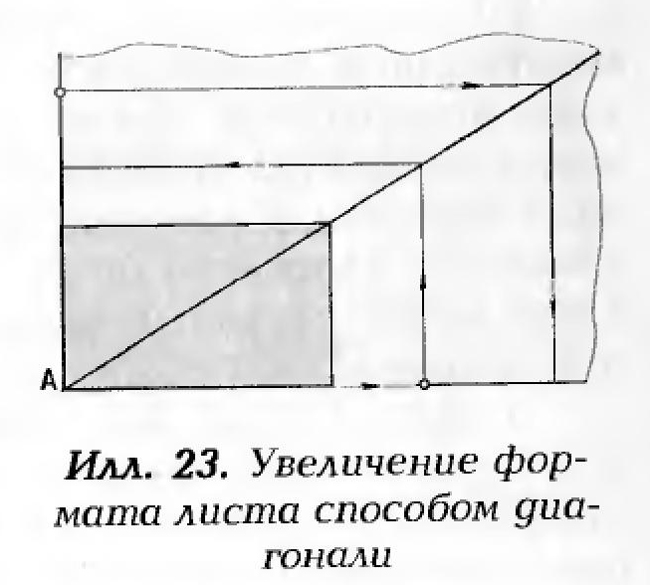Для этого его накладывают на лист бумаги в один из его углов (А) и проводят в нём диагональ. Затем от точки А откладывают заданный размер горизонтальной или вертикальной стороны формата листа и через его конец проводят перпендикуляр до пересечения с диагональю, которая определит вторую сторону прямоугольника.
Источник: М.Н. Макарова «Практическая перспектива»
nata-nedizainer.livejournal.com
